zadanie karol: Znajdź wzór funkcji liniowej której wykres przechodzi przez punkt (0,−1) i jest styczny do paraboli y=x² . Podaj współrzędne punktu styczności. PS. Rozwiązałem to zadanie ale zastanawia mnie czy jest jakiś inny sposób niż rozwiązanie tego z pochodnych. Z góry dziękuje za pomoc

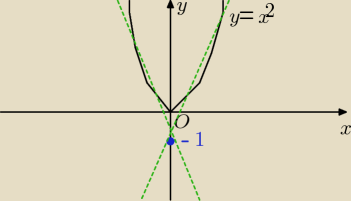
rumpek: Nie wiem czy tak można ale wynik chyba poprawny wychodzi Wzór na funkcje liniową: y = ax + b Styczny czyli przechodzi przez jakiś punkt na y = x² Jeden punkt mamy: (0,−1) oraz drugi (x,y) ⇔ (x,x²)

⎧	y = ax + b
⎩	y = ax + b

⎧	b = − 1
⎩	x2 = ax + b

⎧	b = − 1
⎩	x2 = ax − 1

Teraz zajmijmy się funkcją kwadratową: x² = ax − 1 x² − ax + 1 = 0 Warunek : Δ ≥ 0 Δ = a² − 4 a² − 4 ≥ 0 (a − 2)(a + 2) ≥ 0 Czyli a = 2 v a = −2 Chyba tak chociaż głowy nie dam ściąć Czyli y = −2x − 1 v y = 2x − 1

arek: Dobrze,dzięki !

karol: Tak jest w odpowiedziach dzięki rumpek Widze, że Arkowi też się przydało