Oblicz przyprostokątne CB oraz AC Raqur: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Poprowadzono w tym trójkącie prostą równoległa do przeciwprostokątnej, która przecięła bok AC w punkcie D i bok BC w punkcie E. Oblicz długości przyprostokątnych trójkąta ABC wiedząc, że |DE|=a, |∢ABC|=|∢DAE|=α

Godzio: Zaraz pomogę, bo wydaje się fajne

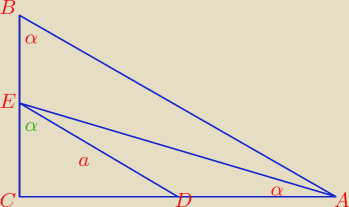
Godzio: Trójkąt DEC:

	|CE|
cosα =		⇒ |CE| = a * cosα
	a

	|CD|
sinα =		⇒ |CD| = a * sinα
	a

Trójkąt AEC:

	|AC|
ctgα =		⇒ |AC| = a * cosαctgα
	|CE|

Trójkąty DEC i ABC są podobne (k,k,k) :

|CD|		|CE|		a * cosαctgα
	=		⇒ |BC| =		= ...
|AC|		|BC|		a * sinα * a * cosα

Godzio:

	a * cosα * ctgα * a * cosα
|BC| =		−− tak powinno być
	a * sinα

Raqur: dzieki

Raqur: nie kumam troche z tym ctg,

Raqur: aaa juz wiem