awdawdawd karolajnn: Dana jest funkcja f(x)= −|x²−2|x|−3|+2 , x∊R Mógłby ktoś dla mnie rozpisać to, żebym mogła ją narysować, a potem wykonać polecenia.

Grześ: Wolisz przedstawienie graficzne, czyli jakie przekształcenia po kolei Czy chcesz algebraicznie, czyli rozpatrywać funkcję przypadkami i rysować kawałkami

karolajnn: Tak rozpatrywać funkcję przypadkami, tzn. f1(x)= −x²+2x+3 dla x≥0 f2(x)= −x²+2|x|−3+2 soy

Qba101: I − x≥0 f(x)= −|x²−2x−3|+2 II − x<0 f(x)= −|x²+2x−3|+2 ♣ I − x≥0 i x²−2x−3≥0 Δ=4+12 x₁=−1 x₂=3 x∊(−∞,−1≥u<3,+∞) ale x≥0 więc x∊<3,+∞) f(x)=−x²+2x+3+2 lub ♣II − x<0 i x²+2x−3<0 x∊(−3,1) ale x<0 stąd x∊(−3,0) f(x)= x²+2x−3+2 ♣ III − x≥0 x²−2x−3<0 x∊(−1,3) ale x≥0 więc x∊(0,3) f(x)= x²−2x−3+2 ♣ IV − x<0 x²+2x−3≥0 x₁=1 x₂=−3 x∊(−∞, −3>u<1,+∞) ale x<0 więc x∊(−∞, −3> f(x)=−x²−2x+3+2 uff... mam nadzieje że bez błędu...

karolajnn: Czy mógłby mi to ktoś narysować ? f1(x)= x²−2x−3 f2(x)=x²−2|x|−3 f3(x)=|x²−2|x|−3| f4(x)= −|x²−2|x|−3| f5(x)= −|x²−2|x|−3|+2 Przekształcenia są raczej poprawne, tylko rysunek nie chce się zgodzić z odpowiedzią.

Godzio: 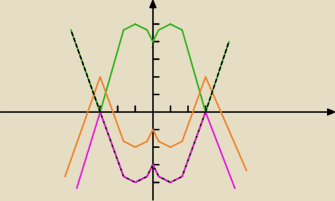2. 3. 4. 5.

karolajnn: właśnie sam odkryłem błąd w obliczeniach. 4 razy 1= 4, nie 8 , ale dzięki.

karolajnn: określ znak liczby f(−4) razy f(−1) + f(−3) Czy istnieje jakiś sposób żeby to zrobić nie obliczając wszystkiego ?