
 W urnie jest 5 kul białych 2 czerwone i 3 czarne Losujemy kolejno dwie kule Jakie jest
prawdopodobienstwo wylosowania dwóch kul tego samego koloru wiedzac ze wylosowana kula za
pierwszym razem nie wraca do urny przed wylosowaniem drugiej kuli.
W urnie jest 5 kul białych 2 czerwone i 3 czarne Losujemy kolejno dwie kule Jakie jest
prawdopodobienstwo wylosowania dwóch kul tego samego koloru wiedzac ze wylosowana kula za
pierwszym razem nie wraca do urny przed wylosowaniem drugiej kuli. Proszę o pomoc oraz wyjaśnienie danego problemu jak wogole podejśc do takiego typu zadań
Proszę o pomoc oraz wyjaśnienie danego problemu jak wogole podejśc do takiego typu zadań
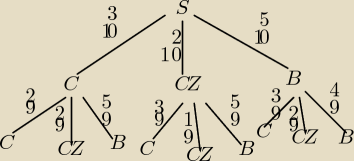 Rozwiązuje się to tak zwanym "drzewkiem" stcośtam. W sumie mamy 10 kul. Jak widać na rysunku
suma prawdopodobieństw wynosi jednego losowania wynosi 1. Zasada jest taka: to co znajduje się
na jednej gałęzi − wymnażamy, a gałęzie ze sobą sumujemy.
Czyli nas interesuje: prawd. wylosowania kul tych samych kolorów czyli może być CC, CZCZ, BB i
tylko to czyli szukamy na rysunku tego wszystkiego i mamy: Czarne kule: 3/10*2/9, Czerwone:
2/10*1/9, Białe: 5/10*4/9 i wszystko sumujemy: 5/90+2/90+20/90=27/90 to się da skrócić i to
jest wynik!.
Rozwiązuje się to tak zwanym "drzewkiem" stcośtam. W sumie mamy 10 kul. Jak widać na rysunku
suma prawdopodobieństw wynosi jednego losowania wynosi 1. Zasada jest taka: to co znajduje się
na jednej gałęzi − wymnażamy, a gałęzie ze sobą sumujemy.
Czyli nas interesuje: prawd. wylosowania kul tych samych kolorów czyli może być CC, CZCZ, BB i
tylko to czyli szukamy na rysunku tego wszystkiego i mamy: Czarne kule: 3/10*2/9, Czerwone:
2/10*1/9, Białe: 5/10*4/9 i wszystko sumujemy: 5/90+2/90+20/90=27/90 to się da skrócić i to
jest wynik!.
 da sie jaśniej
da sie jaśniej 


 przez omege
przez A zdarzenie losowe
przez omege
przez A zdarzenie losowe bo coś czuje ze jak by był wiekszy przykład to nie dało by rady takiego czegos obskoczyc
dzrewkiem
bo coś czuje ze jak by był wiekszy przykład to nie dało by rady takiego czegos obskoczyc
dzrewkiem  !
!
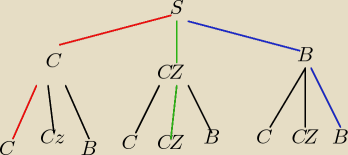 To co masz jednym kolorem np. Czerwonym to wymnażasz, wymnażasz te prawdopodobieństwa bo są na
jednej gałęzi. Ciebie interesują 3 rozwiązania bo chcesz wylosować dwie kule tego samego
koloru czyli albo 2 czarne albo 2 czerwone albo dwie białe(na rysunku zaznaczone).Więc
najpierw wymnażasz pojedyńcze gałęzie: losujesz najpierw czarną i potem znowu czarną:3/10*2/9,
lub najpierw czerwoną potem czerwoną: 2/10*1/9 lub białą a potem białą 5/10*4/9 i wszystko ze
sobą sumujesz.
To co masz jednym kolorem np. Czerwonym to wymnażasz, wymnażasz te prawdopodobieństwa bo są na
jednej gałęzi. Ciebie interesują 3 rozwiązania bo chcesz wylosować dwie kule tego samego
koloru czyli albo 2 czarne albo 2 czerwone albo dwie białe(na rysunku zaznaczone).Więc
najpierw wymnażasz pojedyńcze gałęzie: losujesz najpierw czarną i potem znowu czarną:3/10*2/9,
lub najpierw czerwoną potem czerwoną: 2/10*1/9 lub białą a potem białą 5/10*4/9 i wszystko ze
sobą sumujesz.
| 5 | 4 | 2 | 1 | 3 | 2 | 28 | 14 | |||||||||
P(A)= | * | + | * | + | * | = | = | |||||||||
| 10 | 9 | 10 | 9 | 10 | 9 | 90 | 45 |
 za każdym razem musze poprostu zmniejszyc mianownik bo zostaje
jedna kula odebrana no i wzalezności do którego koloru chce utworzyc pare to pomniejszamy
równiez licznik
za każdym razem musze poprostu zmniejszyc mianownik bo zostaje
jedna kula odebrana no i wzalezności do którego koloru chce utworzyc pare to pomniejszamy
równiez licznik  ! spoko dzieki ale jak bede miał jeszce jakis problem to napewno napisze
! spoko dzieki ale jak bede miał jeszce jakis problem to napewno napisze
 ! Wesolego
! Wesolego