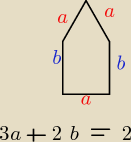:) Adam: okno ma kształt prostokata zakonczonego na gorze trojkatem rownobocnzym Obwod okna wynosi 2m. Jaka powinna byc dlugosc podstawy prostokata, aby przy obwodzie równym 2m powierzchnia okna była największa jak to ugryzc?

Adam: jak to ugryzc?

Godzio: Wylicz z tego a lub b i podstaw do pola:

	a2√3
P = ab +		i policz wierzchołek i dostaniesz wymiary
	4

okok: 2b=2−3a b=1−1,5a

	(1−1,5a)2√3
P= a(1−1,5a) +
	4

	(1−3a+2.25) √3
P= a− 1,5a2 +
	4

	√3 − 3√3a + 2,25√3
P= −1,5a2+a +		/*4
	4

P= −6a² + 4a + √3 − 3√3a + 2,25√3

Adam: −6a²+4a −0,75√3a + √3 ?

Adam: kurcze jak to ma byc

Adam: napisze mi ktos porawne rozwiazanie? bo pierwiastki wychodza

Adam:

Adam:

Adam: jak to ma byc?

Godzio:

	2 − 3a
b =
	2

	2a − 3a2		a2√3		4a − 6a2 + a2√3
P =		+		=		=
	2		4		4

	√3 − 6
a2 *		+ a
	4

	−1		2		2√3 + 12		2√3 + 12
aw =		= −		= −		=
	√3 − 6   2		√3 − 6		3 − 36		33

Chyba się nie pomyliłem

Adam: nie pomyliles sie

Adam: dziks