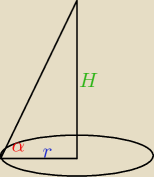
Stożek shogo: Objętość stożka jest równa 1000π, a tworząca tworzy z jego podstawą kąt 30^o. Oblicz pole powierzchni bocznej tego stożka. Pomoże ktoś doszedłem do miejsca: układ równań:

1
	πR2h=1000π
3

h		√3
	=
r		3

i dalej mam takie coś ale nie wiem co dalej zrobić

√3
	πr3=1000π
9

M4ciek:

	1
V =		πr2H
	3

	1
1000π =		πr2H
	3

	r2*H
1000 =
	3

3000 = r²*H

	3000
H =
	r2

	H
tg 30o =
	r

√3		H		√3r
	=		⇒ 3H = √3r ⇒ H =
3		r		3

√3r		3000
	=
3		r2

√3r³ = 9000 r³ = 3000√3 r³ = 1000 * 3 * 3^1₂ / ³√ r = 10 * 3^1₃ * 3^1₆ r = 10 * 3^3₆ r = 10√3

	3000		3000
H =		⇒		= 10
	r2		300

r² + H² = l² l² = 100 + 300 = 400 l = 20 P_b = π*r*l P_b = 200√3π

M4ciek: Odpowiedź pasuje ?

shogo: o ja to miało być z ułamkami w potędze wielki dzięki nie mogłem zrozumieć właśnie jak pozbyć się pierwiastka sześciennego. WIELKIE DZIĘKI

M4ciek: Z drugiej strony tak patrzę to łatwiej było policzyć H , a nie się męczyć z r i potem nie z pitagorasa tylko :

	H
sin 30o =		i mamy l
	l

shogo: Tak masz rację licząc H jest szybciej

M4ciek: Ale jak policzysz r to +10 do lansu