Prosze Pomóżcie;( Kiniaa: Napisz równanie prostej przechodzącej przez punkt A(1,3) i tworzącej z prostą 2x − y = kąt 45stopni.

Kiniaa: Pomoże Ktoś

ICSP: ale w czym ty tutaj masz problem

ICSP: Uwielbiam takie zadanka y = −3x + 6

	1		2
y =		x + 2
	3		3

Chyba tak. W pamięci liczyłem to mogłem się pomylić.

Kiniaa: Ale on ma tworzyć kąt 45 stopni a nie 90 .

Kiniaa: mogę wiedzieć jak to policzyłeś?

ICSP: widzę że warunek prostopadłości znasz Jednak są dwie proste które tworzą z prostą y = 2x kąt 45^o.

ICSP: Mów w którym momencie zadania utknęłaś.

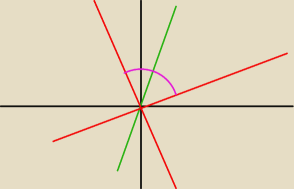
ICSP: Jak widzisz czerwone proste są do siebie prostopadłe gdyż tworzą z zieloną prostą dwa katy po 45^o

Kiniaa: Ja w ogóle nie wiem jak to zacząć. Prosta k; y = 2x więc prosta prostopadła do niej to

	1
k'; y = −		x + b
	2

i nie mam pojęcia jak to zrobić.

ICSP: a₁ = 2 a₂ = ?

	a1 − a2
1 = |		|
	1 + a1 * a2

Wylicz z tego a₂ i następnie wstaw współrzędne punktu .Dwie pionowe kreski to wartość bezwzględna dlatego będą dwa rozwiązania.

Kiniaa:

	a1 − a2
Ale z kąt się to wzięło: 1 = I		I ?
	1 + a1 * a2

ICSP: Wzór na kąt między prostymi.

ICSP: https://matematykaszkolna.pl/strona/1228.html

Kiniaa: A dało by się to obliczyć bez tego wzoru Ja go jeszcze nie brałam.

ICSP: Wzorem jest najszybciej i najbezpieczniej. Jak chcesz bez niego możesz próbować kombinować z przekątną kwadratu.

Kiniaa: ok, więc jak liczę ze wzoru to mam :

	2 − a2
I		I = 1
	1 + 2 * a2

	2 − a2		2 − a2
		= 1 lub		= −1
	1 + 2 * a2		1 + 2 * a2

tak

Qba101: https://matematykaszkolna.pl/strona/1228.html

Qba101: ups. przez pomyłkę wkleiłem, sorry

ICSP: Zrobiłem to innym sposobem może wieczorkiem napisze.

ICSP: Już zabieram się zapisanie

ICSP: Czy może już nie potrzeba?

Kiniaa: No jak byś mógł to napisz

ICSP: Troszkę to zajmie

Kiniaa: ok

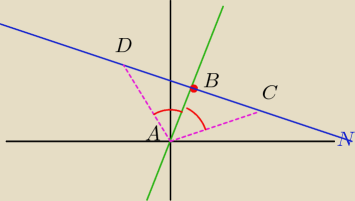
ICSP: krótkie tłumaczenie: Jednostki nie są zachowane stąd brak ich na rysunku. Czerwony punkt ma współrzędne B(2;4) i należy on do zielonej prostej które dana jest w zadaniu : y = 2x niebieska prosta jest prostopadła do prostej zielonej oraz przechodzi przez punkt B. Mozemy

	1
wyznaczyć jej równanie: y = −		x + 5. Sama sobie wyznaczysz.
	2

Długość odcinka AB = 2√5 Jeżeli teraz założymy że odcinek AB jest bokiem kwadratu a różowe jego przekątnymi( każda różowa prosta jest od innego kwadratu ponieważ są tutaj dwa kwadraty: kwadrat ABCX oraz kwadrat ABDY gdzi X i Y są punktami które są dla nas kompletnie nieważne.) |AB| = |BC| = |BD|. Czerwone kąty są takie same i mają po 45^o co zresztą widać z własności kwadratu. Dlatego jeżeli obliczymy współrzędne punktów C oraz D będziemy mogli obliczyć współczynniki kierunkowe tych dwóch prostych. Układamy układ równań:

	1
y= −		x +5
	2

(x−2)² + y(−4)² = 20 Napisanie rozwiązania ukłądu równań zajeło by mi około 15 min chyba że zrobię tak: x = −2 to y = 6 − punkt D na rysunku x = 6 to y = 2 − punkt C na rysunku A(0;0) C(6;2) prosta AC jest nachylona do prostej AB pod kątem 45^o dlatego liczę tylko jej współczynnik kierunkowy.

	2−0		1
a =		=
	6−0		3

i w tym momencie zauważam że punkt A jest dany w zadaniu jako (1;3). Dlatego przerabiam ten punkt A z zadania na punkt E żeby nie psuć wszystkie co do tej pory narysowałem. E(1;3) równanie prostej równoległej do prostej AC przechodzącej przez punkt E:

	1
y =		x + b
	3

	1
3 =		+ b
	3

	2
b= 2
	3

mamy już skończoną jedną prostą: y = ¹₃x + 2²₃ Teraz prosta AD: A(0;0) D(−2;6)

	6−0
a =		= −3
	−2−0

punkt E należyo do tej prostej: y = −3x + b 3 = −3 + b b = 6 y = −3x + 6

Kiniaa: Ok, Dziękuje

ICSP: Jednak chyba lepiej wzorem to robić

Kiniaa: No chyba tak..