Twierdzenie sinusów Sylwia: W trójkącie równoramiennym kąt przy wierzchołku ma miarę 120 stopni. Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.

Sylwia: Niech ktoś pomoże

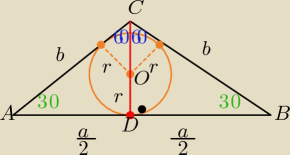
Eta: R −−− dł promienia okręgu opisanego r −−− dł. promienia okręgu wpisanego

	b
ze wzoru sinusów: 2R=
	sin30o

2R= 2b => R= b

	2P
r=
	p

	1		b2√3
P=		*b*b*sin60o =
	2		4

	b2√3
to 2P=
	2

p= a+2b z funkcji trygonom.

	a2
		= sin60o => a= b√3
	b

zatem p= 2b+b√3= b(2+√3)

	b√3
r= ............ =
	2(2+√3)

	R		2(2+√3)
		= b*		= ........ dokończ
	r		b√3