 Witam, mam problem z tym zadaniem:
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy większa od drugiej. Wykaż , że
wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy
większy od drugiego.
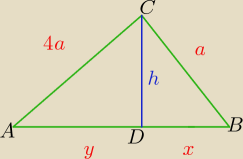
Mam rozwiązania, jednak nie wiem jak do tego podejść, zrobiłem taki rysunek:
Mam wykazać, że y=16x
Wiem, że trójkąty ABC, ADC, BCD są podobne jednak nie wiem na jakiej zasadzie. Proszę o pomoc.
Witam, mam problem z tym zadaniem:
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy większa od drugiej. Wykaż , że
wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy
większy od drugiego.
Mam rozwiązania, jednak nie wiem jak do tego podejść, zrobiłem taki rysunek:
Mam wykazać, że y=16x
Wiem, że trójkąty ABC, ADC, BCD są podobne jednak nie wiem na jakiej zasadzie. Proszę o pomoc.
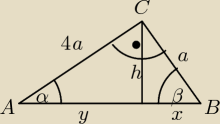
| h | ||
tgα= | ||
| y |
| a | 1 | |||
tgα= | = | |||
| 4a | 4 |
| h | 1 | ||
= | |||
| y | 4 |
| y | ||
h= | ||
| 4 |
| h |
| |||||||||
tgβ= | = | |||||||||
| x | x |
| 4a | ||
tgβ= | =4 | |
| a |
| |||||||
=4 | |||||||
| x |
| y | ||
4x= | /*4 | |
| 4 |

 także zamieniłam h na to co wcześniej mi wyszło tak żeby później w równaniu mieć dwie wielkości
aby porównać ich stosunek do siebie
także zamieniłam h na to co wcześniej mi wyszło tak żeby później w równaniu mieć dwie wielkości
aby porównać ich stosunek do siebie