 czy to jest dobrze zrobione
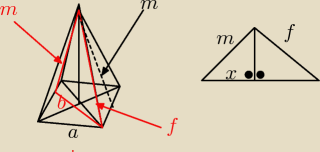
czy to jest dobrze zrobione W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe S, a kąt nachylenia ściany
bocznej do plaszczyzny podstawy ma miare α. Ostrosłup przecieto plaszczyzna zawierajaca
krawedz boczna tego ostroslupa i przechodzaca przez srodek rozlacznej z nia krawedzi podstawy.
Oblicz pole otrzymanego przekroju.
a2=S
a=√S
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe S, a kąt nachylenia ściany
bocznej do plaszczyzny podstawy ma miare α. Ostrosłup przecieto plaszczyzna zawierajaca
krawedz boczna tego ostroslupa i przechodzaca przez srodek rozlacznej z nia krawedzi podstawy.
Oblicz pole otrzymanego przekroju.
a2=S
a=√S
| H | ||
tgα= | ||
| √S |
| √5 | ||
−x) | ||
| 2 |
| √5 | ||
( | −x)2 +h2= S(tg2α+2) | |
| x |
| 25 | ||
z tego wyszlo mi ze h=U{√5S(tg2α+1)− | +S2 | |
| 16 |
| |||||||||||
I wtedy Vprzekroju= | |||||||||||
| 4 |
| H | ||
Nie wiem skąd masz tgα = | bo nie zaznaczylas α, ale jesli to jest kat miedzy sciana
| |
| √S |
| H | ||
boczna (=wysokoscia sciany) a plaszczyzna podstawy, to wtedy tgα = | ||
| a/2 |
| H | ||
i chyba widze swój błąd tam powinno być tgα= | tak  | |
| 1/2a |

 bd to liczyc jeszcze raz
bd to liczyc jeszcze raz