21 kwi 22:55
Atola: jest taki wzór na pole trójkąta, który nazywa się wzór Herona.
21 kwi 22:58
21 kwi 22:58
Atola: Ptrójkąta=√p(p−a)(p−b)(p−c)
p=(a+b+c)/2
a,b,c−długości boków
21 kwi 22:59
roman: aha no zaraz to zastosuje i zobaczę ... sprawdzicie mi później >?
dzięki za wzory ....

21 kwi 23:01
roman:
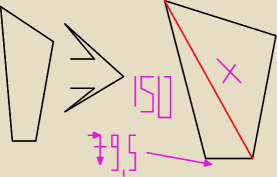
no i co z pitagorasa go czy jak >? bo
do tego wzoru co mi podaliście to potrzebuje trójkąt a to jest czworokąt ,,, więc byłoby go
trzeba jakoś podzielić ....
21 kwi 23:06
Bolek: wzór Herona jest brany pod uwage gdy chcemy obliczyć pole danej figury a mamy tylko jej boki,
wówczas liczymy tzw. połowe tej figury:
p= 1/2(a+b+c+d) ( a,b,c,d) są ta boki tej twojej figury, następnie gdy obliczysz tzw.
połowe pola pwówczs obliczsz całość pola
S=
√p(p−a)(p−b)(p−c)(p−d) to małe p już obliczyłeś sobie wcześniej, więc podstawiasz wartości
boków wymnażasz i wyciągasz z tego pierwiastek i tyle

rozumiesz

22 kwi 08:12
Bolek: Sorki pomyliłem sie, heron jest tylko przy trójkątach

przepraszam

22 kwi 09:26
Ajtek: Użyj tego wzoru:
P=√(p−a)(p−b)(p−c)(p−d), gdzie p to połowa obwodu.
Jest to wzór Brahmagupty.
Bolek podał prawie dokładny wzór, tylko wcisnął niepotrzebnie jedno p, na samym początku pod
pierwiastkiem.
22 kwi 10:54

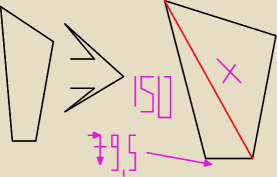 no i co z pitagorasa go czy jak >? bo
do tego wzoru co mi podaliście to potrzebuje trójkąt a to jest czworokąt ,,, więc byłoby go
trzeba jakoś podzielić ....
no i co z pitagorasa go czy jak >? bo
do tego wzoru co mi podaliście to potrzebuje trójkąt a to jest czworokąt ,,, więc byłoby go
trzeba jakoś podzielić ....
 rozumiesz
rozumiesz
 przepraszam
przepraszam