trapez megg57: Punkty A = (0, 3) i D = (3, 4) są wierzchołkami trapezu równoramiennego ABCD. Prosta −x + y + 7 = 0 przechodzi przez punkt C i jest prostopadła do podstaw trapezu. a) oblicz współrzędne pozostałych wierzchołków tego trapezu b) oblicz pole tego trapezu.

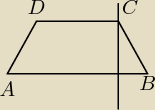
Aga: A = (0, 3) i D = (3, 4) Prosta przechodząca przez punkt C ma równanie: −x+y+7=0 po przekształceniu y=−x−7 jest ona prostopadła to podstawy DC więc możemy obliczyć jej równanie

	−1
a=		=1 więc y=x+b
	−1

Podstawiam współżędne punktu D by wznaczyć b 4=3+b b=1 Mamy równanie prostej CD y=x+1 tworzymy układ równań z tych prostych aby znależć współrzędne punktu C

⎧	y=−x−7
⎩	y=x+1

⎧	y=−x−7
⎩	x=y−1

podstawiamy y do drugiego równania x=−x−7−1 2x=6 x=3 i podstawiamy x do pierwszego równania y=−3−7 y=−10

Aga: Są to współrzędne punktu C, na tej samej zasadzie obliczamy współrzędne punktu B, najpierw równanie prostej AB, potem układ współrzędny tej prostej i prostej prostopadłej przechodzącej przez C

Aga: nie! przepraszam B nie obliczymy z tych prostych

Aga: wyznaczamy równanie prostej AD wstawiając współrzędne ich i tworząc układ równań: 4=3a+b 3=b 4=3a+3

	1
a=
	3

	1
czyli: y=		x+b
	3

	1
analogicznie prosta BC będzie miała równanie y=−		x+b
	3

tworzymy układ równań aby otrzymać współrzędne punktu B prostej AB(jest równoległa no CD więc a zostaje takie samo szukamy b przez podstawienie wpółrzednych A) i prostej BC y=x+3

	1
y=−		x+3
	3

x=y−3

	1
y=−		(y−3)+3
	3

	3
y=
	2

	3
x=−
	2

Aga: teraz aby obliczyć pole potrzebujemy długości odcinków |AB| |CD| oraz wysokości. Obliczymy ich ze wzoru na długość odcinka: |AB|=√(Xb−Xa)² + (Yb−Ya)² tak samo drugi odcinek.Aby obliczyć wysokość musimy obliczyć dlugość odcinka AD aby potem wyznaczyć ją z pitagorasa. Ten

	|AB|−|CD|
odcinek miedzy wysokoscia a np punktem A wynosi		.
	2

	(a+b)h
kiedy mamy wszystkie długości podstawiamy pod wzór na pole trapezu P=
	2

Bardzo przepraszam za takie zamieszanie, mimo wszystko mam nadzieję, że pomogłam.