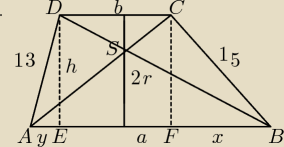
 W trapez o polu 168 i ramionach 13 i 15 można wpisać okrąg. Przekątne dzielą ten trapez na
cztery trójkąty. Oblicz pole każdego z nich.
No i tak:
Wiemy że można wpisać w niego okrąg więc twierdzenie:
a+b=28
Pole=28*2r/2=28r
168=28r
r=6
2r=12
liczymy x i y z pitagorasa:
Trójkąt ADE y=5
Trójkąt BFC x=9
Stąd liczymy a i b bo:
b+14=a
a+b=28
stąd a=21
b=7
No i mając te dane liczę przekątne:
Trójkąt DEB |DB|=20
Trójkąt AFC |AC|=12√2
Tu pojawia się problem, niby mam tyle danych moge sobie obliczyć ACD, BCD, ADB, ACB ale z
żadnego odejmowania pól nie jestem w stanie wyliczyć pojedyńczych trójkątów.
Przypomnę, że chodzi o ASB, DSC, ASD i BSC
Pozdrawiam.
W trapez o polu 168 i ramionach 13 i 15 można wpisać okrąg. Przekątne dzielą ten trapez na
cztery trójkąty. Oblicz pole każdego z nich.
No i tak:
Wiemy że można wpisać w niego okrąg więc twierdzenie:
a+b=28
Pole=28*2r/2=28r
168=28r
r=6
2r=12
liczymy x i y z pitagorasa:
Trójkąt ADE y=5
Trójkąt BFC x=9
Stąd liczymy a i b bo:
b+14=a
a+b=28
stąd a=21
b=7
No i mając te dane liczę przekątne:
Trójkąt DEB |DB|=20
Trójkąt AFC |AC|=12√2
Tu pojawia się problem, niby mam tyle danych moge sobie obliczyć ACD, BCD, ADB, ACB ale z
żadnego odejmowania pól nie jestem w stanie wyliczyć pojedyńczych trójkątów.
Przypomnę, że chodzi o ASB, DSC, ASD i BSC
Pozdrawiam.
| a | ||
ΔABS ~ Δ CDS w skali: k= | = 3
| |
| b |
| 3 | ||
zatem dla ΔABS h1= | *h= 9
| |
| 4 |
| 1 | ||
dla ΔCDS h2= | h= 3
| |
| 4 |
| a*h1 | ||
P ΔABS= | =..........
| |
| 2 |
| b*h2 | ||
PΔCDS= | =.........
| |
| 2 |

 .
.


 moze mi ktos to powiedzieć? wystepuje to na poczatku obliczen
zajaczka
moze mi ktos to powiedzieć? wystepuje to na poczatku obliczen
zajaczka
| h1 | ||
sin45 stopni = | ||
| 3x |
| √2 | h1 | ||
= | |||
| 2 | 9√2 |
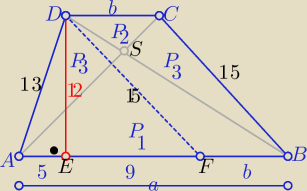 Z warunku wpisania okręgu w trapez : a+b=28
P(trapezu) =14*h= 168 ⇒ h=12
Z tw. Pitagorasa w ΔAED i DEF ⇒ |AE|=5 i |EF|=9 to b=7 więc a= 21
Z warunku wpisania okręgu w trapez : a+b=28
P(trapezu) =14*h= 168 ⇒ h=12
Z tw. Pitagorasa w ΔAED i DEF ⇒ |AE|=5 i |EF|=9 to b=7 więc a= 21
| a | ||
ΔABS i ΔDCS są podobne w skali k= | =3 | |
| b |

