ff MARTA: Jeden z końców odcinka leży na paraboli o równaniu y = x2 , a drugi na prostej o równaniu y = 2x − 6 . Wykaż, że długość tego odcinka jest nie mniejsza od 5 . prosilabym o [pomoc

MARTA: od √5 !

Sabin: Czy znasz wzory na wierzchołek funkcji kwadratowej oraz na odległość punktu od prostej?

MARTA: no niby

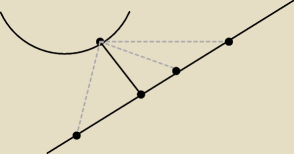
Sabin: Zauważ, że najkrótszy z tych odcinków będzie ten, który jest poprowadzony pod kątem prostym do prostej − czyli będzie odległością punktu na paraboli od prostej. Oznaczmy punkt na paraboli przez A. Wtedy A = (x_A, x_A²). Dalej zamiast x_A będę pisał a − jestem leniwy. Prostą, nazwijmy ją k: y = 2x − 6 zapisujemy jako k: 2x − y − 6 = 0

	|2a − a2 − 6|
Wtedy odległość tych punktów − ze wzoru, to: d(A, k) =		=
	√5

	|a2 − 2a + 6|
=
	√5

Ta odległość będzie najmniejsza wtedy, gdy najmniejszy będzie licznik − a tak będzie w wierzchołku paraboli z licznika. Wierzchołek ma współrzędne x_w = 1 y_w = 5. Czyli najmniejsza wartość licznika to 5 − stąd najmniejsza wartość całego ułamka to ⁵_√5 = √5. Każda inna jest większa.