Bardzo Proszę o Pomoc. Agula: Napisz równanie dwusiecznych kątów zawartych pomiędzy prostymi a) k; y = 2x + y l; y = 3x + 1 b) k; x − y +1 = 0 l; y = 4x +2

Agula: Proszę pomóżcie

włóczykij: w przykładzie a jest bład w prostej k nie ma być y= 2x + y tylko + coś innego

włóczykij: mam racje

Agula: Nie. Powinno byc tak jak jest.

włóczykij: więc tak przykład a to y= 6x+1

Agula: A mogła bym Prosić o wyjaśnienie.

Agula:

ICSP: czy aby na pewno jest tylko jedna taka prosta?

Kejt: no właśnie.. dwie..

włóczykij: więc tak jedna z tych prostych to będzie oś OY a druga przechodzi przez punkty (2,7) i (0,1) czyli przcinają sie w punkcie A(0,1) a między nimi trzeba znależć punkt na środku gdzieś obojętnie gdzie. najlepiej sobie narysować i tak punkt równo oddalony w górze między nimi to np B(1,7) i teraz obliczamy ze wzoru na prostą przechodzącą przez te dwa punkty A i B i to jest ich dwusieczna

Agula: Nom, właśnie powinny wyjść dwie proste.

włóczykij: w każdym podpunkcie będzie jedna prosta bo kąty będą dwa wierzchołkowe a ich dwusieczne leżą na tej samej prostej

włóczykij: a podpunktu b nie obliczyłem

włóczykij: acha rzeczywiście przepraszam jeszcze po jednej prostej powinny wyjść tych kątów rozwartych ale jak wie sie jak poprzedniego obliczałem to już łatwe

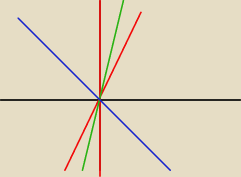
ICSP: troszke źle ale ja tutaj widzę dwie proste. Oś OX powinna być o jedna jednostkę w dół.

Agula: Która prosta to y = 2x + y , a która y = 3x + 1

włóczykij: y= 2x+y to oś OY czyli pionowa a y= 3x +1 to czerwona pochylona

ICSP: y = 2x + y ⇔ 2x = 0 ⇔ x = 0Prosta o takim równaniu jest ci bardziej zwana pod nazwą osi OY

ICSP: tylko jak już mówiłem. Oś OX powinna być o jedna jednostkę w dół obniżona. Poprostu coś mi sie pomyliło przy rysowaniu

Agula: Ok, ale i tak dalej nie wiem jak napisać to równanie dwusiecznych .

włóczykij: to są te zielona i niebieska

Agula: Ale jak ja mam wyznaczyć równanie tych dwusiecznych? Mam wskazówkę zeby liczyć to z warunku: d(P,k) = d(P,l)

Agula: d(P,k) = d(P,l) p=(x,y)

IxI		I3x − y + 1 I
	=
√1		√9 +1

IxI		I3x − y + 1 I
	=
1		√10

	I3x − y + 1 I
IxI =		⇒
	√10

	I3x − y + 1 I		I−3x + y −1 I
⇒ IxI =		lub IxI =
	√10		−√10

√10x = 3x − y + 1 −√10x = −3x +y − 1 3x − √10x − y + 1 = 0 −3x + √10x + y − 1 = 0 Może tak być?

Agula: Wyleciało mi : ile to jest 3 − √10

ICSP: to jest <0 bo 10 jest > 9

Agula: ok, a dobrze to jest zrobione

Agula: b)

Ix − y +1 I		I 4x − y +2 I
	=
√1 + 1		√16 + 1

Ix − y +1 I		I 4x − y +2 I
	=
√2		√17

I nie wiem jak dalej..

zajączek: opuść moduły bez zmiany znaków , otrzymasz równanie jednej dwusiecznej opuść drugi ze zmianą znaków, a pierwszy bez zmiany , otrzymasz równanie drugiej dwusiecznej rachunki paskudne, ale da się policzyć