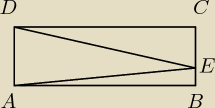
3 pytanka. Gondzio :D poświęć troche czasu... Artur: Gondzio... 1Dotyczące rysunku, Trzeba wykazać ze kąt BAE+ EDC = AED czy w takim dowodzie można po prostu napisać ze ramiona kąta AED leżą na odcinku AD o pewnej długości, tak samo jak w sumie kąt BAE i EDC? i z racji ze AD = BC to wykazałem? 2Było dzisiaj w wyborczej takie zadanko. Dane są punkty A (0 0) B(4 6) C (12 −8) Wykaż ze trójkąt ABC jest prostokątny. Postanowiłem wyliczyć Proste i porównać współczynniki i wyjdzie ze któraś pada pod kątem prostym..ale nie wyszło... AB: y=3/2x AC:y=−3/4x BC:y=−7/4x + b Coś źle podstawiłem? dobrze myślałem z tym zadankiem? 3 chodzi mi o zadanka z wielomianami, w stylu ze " reszta z dzielenia W(x) przez jakiś tam wielomian jest trójmianem i ze trzeba wyznaczyć resztę z dzielenia" zadania w tym stylu, przegrzebałem tą stronke ale nie znalazłem przykładów twierdzen z których można zrozumieć takie zadania....Może nie zauważyłem? Albo wytłumaczyć co powinienem robić?

Godzio: 1. Dowód to jeszcze nie jest.

	3		2
2. AB: a =		AC: a1 = −
	2		3

AB jest prostopadłe do AC bo a * a₁ = −1 3. Reszta z dzielenia W(x) przez dwumian (x − 2) wynosi 5 to znaczy, że: W(2) = 5 W(x) = Q(x)(x − a) + R(x) ⇒ W(a) = R(a) Reszta z dzielenia W(x) przez (x − 1) jest 6, przez (x − 2) jest 3, wyznacz resztę z dzielenia x² − 3x + 2 x² − 3x + 2 = (x − 1)(x − 2), z polecenia wiemy ze W(1) = 6, W(2) = 3 Więc: W(x) = Q(x)(x − 1)(x − 2) + ax + b (reszta może być co najwyżej o jeden stopień mniejsza) W(1) = a + b = 6 W(2) = 2a + b = 3 odejmuję stronami: −a = 3 a = −3 ⇒ b = 9 R(x) = −3x + 9 Coś tego typu jest

Bizon: ∡ DAE=90^o−∡ BAE ∡ ADE=90^o−∡ CDE ∡ AED=180^o−∡ DAE−∡ ADE=180^o−90^o+∡ BAE−90^o+∡ CDE=∡ BAE+∡ CDE ∡ AED=∡ BAE+∡ CDE

Artur: ok. Może ktoś podrzuci jakieś zadanko z Wielomianem? Godzio?

Kejt: możesz się poczęstować: https://matematykaszkolna.pl/forum/91921.html na zdrowie