oblicz objętość w graniastosłupie prawidłowym sześciokątnym agaaa: Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 60 stopni. Wiedząc że podstawę graniastosłupa można wpisać w koło o promieniu 2√3. Oblicz objętość tego graniastosłupa

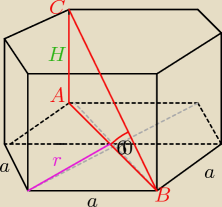
Aska: kąt CAB=90^o |AB|=2r=4√3 a=r=2√3 H=|CA|=4√3{3}=4*3=12 (ponieważ bok CA leży naprzeciwko kątowi 60^o i jest to 2r√3)

	3a2√3
Pp=
	2

V=H*Pp

	3*(2√3)2*√3
V=12*		=6*3*4*3*√3=216√3
	2