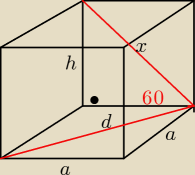
 powiedzmy6że to graniastosłup prawidłowy czworokątny czyi ma w podstawie kwadrat
d=a√2
a=2√2
x=2a=4√2
powiedzmy6że to graniastosłup prawidłowy czworokątny czyi ma w podstawie kwadrat
d=a√2
a=2√2
x=2a=4√2
| x√3 | |
=h | |
| 2 |
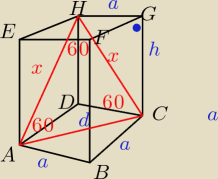 rysunek jest mało ważny. wracając z banku myślałam jak je rozwiązać i doszłam do wniosku że
należy dorysować drugą przekątną i w ten sposób wyjdzie trójkąt równoboczny
bo x jest przekątną ściany bocznej a wszystkie są przystające
zatem kąty CAH i HCA sa takie same bo to trójkąt równoramienny i przy podstawie będzie po 60
stopni. Suma kątów w trójkącie jest równa 180 stopni z czego wynika że kąt AHC jest również
równy 60 stopni. mamy więc do czynienia z trójkątem równobocznym o czym już wcześniej
wspomniałam
d=a√2
stąd a=2p{2]
d=x
i z twierdzenia pitagorasa
a2+h2=x2
h=2√2
V=Pp*h=8*2p{2]=16√2[j3]
mam nadzieję że to będzie tak
rysunek jest mało ważny. wracając z banku myślałam jak je rozwiązać i doszłam do wniosku że
należy dorysować drugą przekątną i w ten sposób wyjdzie trójkąt równoboczny
bo x jest przekątną ściany bocznej a wszystkie są przystające
zatem kąty CAH i HCA sa takie same bo to trójkąt równoramienny i przy podstawie będzie po 60
stopni. Suma kątów w trójkącie jest równa 180 stopni z czego wynika że kąt AHC jest również
równy 60 stopni. mamy więc do czynienia z trójkątem równobocznym o czym już wcześniej
wspomniałam
d=a√2
stąd a=2p{2]
d=x
i z twierdzenia pitagorasa
a2+h2=x2
h=2√2
V=Pp*h=8*2p{2]=16√2[j3]
mam nadzieję że to będzie tak