;) donka: w ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do podstawy pod kątem 60 stopni i ma długość 10cm. Oblicz ppc i v tego ostrosłupa.

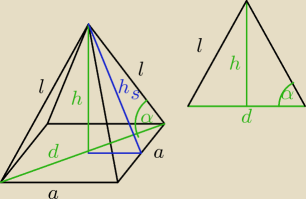
dero2005: l = 10 α = 60^o

h		√3
	= sin 60o =
l		2

	l√3		10√3
h =		=		= 5√3 → wysokość
	2		2

d2		1
	= cos 60o =
l		2

d = l = 10 → przekątna podstawy 2a = d²

	d√2		10√2
a =		=		= 5√2 → krawędź podstawy
	2		2

h_s = √(^a₂)² + h² = √(⁵₂√2)² + (5√3)² = ⁵₂√14 P_p = a² = (5√2)² = 50 → powierzchnia podstawy P_b = 2*a*h_s = 2*5√2*⁵₂√14 = 50√7 → powierzchnia boczna P_c = P_p + P_b = 50 + 50√7 = 50(1 + √7) → powierzchnia całkowita

	250
V = 13Pp*h = 13* 50 * 5√3 =		√3 → objętość
	3

Karo: Czy można zapisać a właściwie obliczyć w inny sposób Hs np.

	(5√2)2
Hs2 =		+ (5√3)2
	2

	100
Hs2 =		+ 75 = 50 + 75 = 152
	2

Hs² = 125 Hs = √125 czy idąc tym tokiem rozumowania i rozwiązywania zadania doszedłbym do tego samego wyniku który ty podałeś?

Karo: odświeżam.

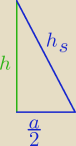
dero2005: nie rozumiem co to za działania przecież tam jest trójkąt prostokątny i wystarczy zastosować Pitagorasa

Karo: po prostu nie rozumiem Twojego zapisu na Hs dlatego chciałem się Cb zapytać czy można w jakiś inny sposób dojść do tego

	5
wyniku, który podałeś		√14
	2

Karo: pomoże mi ktoś zrozumieć skąd wyszedł taki a nie inny wynik na Hs?

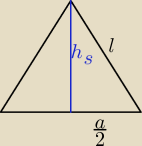
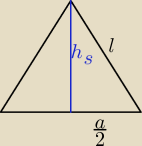dero2005: można l = 10 ^a₂ = ⁵₂√2 z Pitagorasa h_s = √l² − (^a₂)² = √10² − (⁵₂√2)² = √100 − ⁵⁰₄ = √³⁵⁰₄ = = √^25*14₄ = ⁵₂√14