Oblicz promień okręgu :): Czworokąt ABCD wpisany w okrąg. Oblicz promień jeżeli AB=AC=4 oraz CD=BC=6

izi: nie zrobiłaś przypadkiem błędu? na pewno AB i AC, a nie AB i AD?

:): o sora miało być AB=AC i BC=CD. Wiem że wynik jest √13 ale nie wiem jak do tego doszło.

:): Jeju. Znowu pomyłka. Nie umiem łanie przepisać AB=AC i BD=CD.. Jej Tym razem chyba sie nie pomyliłam.

:): Jeju. Znowu pomyłka. Nie umiem łanie przepisać AB=AC i BD=CD.. Jej Tym razem chyba sie nie pomyliłam.

izi: hm. sprawdź dokładnie, bu chyba powinno być AB=ac i CD=BC. odcinki typu BD odpadają, bo to już by były przekątne narysuj sobie prostokat w okręgu i pozaznaczaj długości boków a także przekątne tego prostokąta. owa przekatna to bedzie srednica okręgu jeśli ją wyliczysz ze wzoru wystarczy podzielić przez dwa i wyjdzie promień okręgu.

:): to nie może być prostokąt bo Ab=4 a Cd=6. własnie coś jest z tymi przekątnymi ale nie wiem co.

:): to nie może być prostokąt bo Ab=4 a Cd=6. własnie coś jest z tymi przekątnymi ale nie wiem co.

izi: to chyba nie pomogę:(

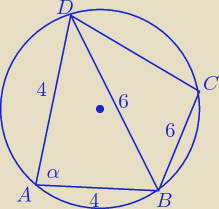
Godzio: Rozpatruje trójkąt ABD: z tw. cosinusów: 16 + 16 − 32cosα = 36 −32cosα = 4

	1		√65
cosα = −		⇒ sinα = √1 − (1/8)2 =
	8		8

Z tw. sinusów:

6
	= 2R
sinα

	3		24		24√65
R =		=		=
	sinα		√65		65

Godzio: Teraz widzę, że treść źle przeczytałem , trochę zamieszania było, zaraz poprawie

Godzio: Dla pewności: AB=AC = 4 i BD=CD = 6 ?

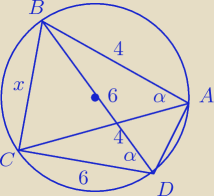
Godzio: Z tw. cosinusów dla trójkątów: CDB i ABC : x² = 16 + 16 − 32cosα x² = 36 + 36 − 72cosα − −−−−−−−−−−−−−−−−−−−−−−−− 0 = 32 − 72 − 32cosα + 72cosα 40 = 40cosα cosα = 1 Możliwe ? Wątpię... coś nie tak z treścią