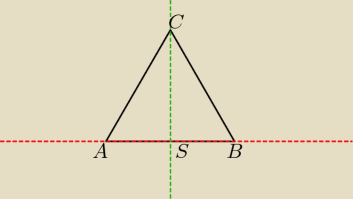
geometria analityczna Glourious: Zadanie z serii 'nie rozumiem' Bardzo bym prosił o rozwiązanie, z opisanymi rzeczami które są liczone i z czego liczone A więc tak: Podstawa AB trójkąta równobocznego ABC zawarta jest w prostej y= ³₄ x + 1, a wierzchołek C= −1,4 . Wyznacz współrzędne A i B tego trójkąta Zadanie maturalne na 6 pkt, poziom podstawowy

rumpek: Prosta:

	3
y =		x + 1
	4

Czyli punkty A i B mają postać:

	3
A(x,		x + 1)
	4

	3
B(x,		x + 1)
	4

Liczysz prostą przechodzącą przez punkt C i zarazem prostopadłą do prostej y. a₁ * a₂ = −1

	4
a2 = −
	3

	4
y = −		x + b
	3

	16
−1 = −		+ b
	3

	3		16
b = −		+
	3		3

	13
b =
	3

	4		13
y = −		x +
	3		3

Proponuje jeszcze przeliczyć Liczysz teraz punkt S układem równań:

⎧	y = 3/4 x + 1
⎩	y = −4/3 x + 13/3

Jak wyznaczysz ten punkt S to potem liczysz odległość CS (to będzie wysokość) i dalej z twierdzenia Pitagorasa |CS|² + |SB|² = |CB|²

	3
pamiętając o B(x,		x + 1)
	4

|SB| − odległość Jak to obliczysz podobnie robisz punkt A Powinno wyjść Ale jeszcze raz powtórzę: przelicz tę prostą którą liczyłem

Bizon: −skoro trójkąt jest równoboczny to IABI=IACI=IBCI −dodatkowo punkty A i B leżą na prostej y=U{3{{4}x+1 ... ich współrzędne spełniają więc równanie prostej ... Cztery na cztery ...

Glourious: dziękuje

rumpek: Bądź mona jeszcze spróbować jak miałeś odległość prostej od punktu

	3
wtedy liczysz odległość punktu C od prostej y =		x + 1 to będzie wysokość, a wzór na
	4

wysokość w trójkącie równobocznym jest a√3 więc bez problemu liczysz bok i dalej podobnie jak wyżej