Twierdzenie sinusów
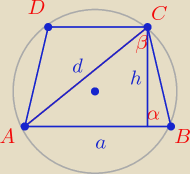
Sylwia: Trapez ABCD (AB || CD, |AB|>|CD|) jest wpisany w okrąg o promieniu R. Wiadomo, że kąt ostry
tego trapezu ma miarę α, zaś |∡ACB|=β, gdzie AC jest przekątną trapezu. Oblicz długość h
wysokości trapezu.
17 kwi 00:43
Godzio:
| | 1 | | 1 | |
PΔ = |
| adsin(180 − (α + β) ) = |
| * 2Rsinβ * 2Rsinα * sin(α + β) = |
| | 2 | | 2 | |
= 2R
2sinβsinαsin(α + β)
| | ah | | 2Rsinβ * h | |
PΔ = |
| ⇒ 2R2sinβsinαsin(α + β) = |
| ⇒ h = Rsinαsin(α + β) |
| | 2 | | 2 | |
17 kwi 00:49
Sylwia: Jaki z Ciebie mózg...
17 kwi 00:58
Sylwia: | | 1 | |
A dlaczego tam jest |
| * a * d  Skąd tam się wzięło to d  |
| | 2 | |
17 kwi 01:02
;):
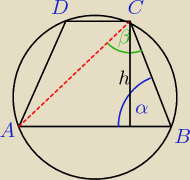
|AC| = 2sinαR
|AB| = 2sinβR
| | |AC| * |AB| | |
PΔACB = |
| * sin(α + β) = 2sinαsinβsin(α + β)R2 |
| | 2 | |
| | 1 | | PΔACB | |
PΔACB = |
| * |AB| * h h = |
| |
| | 2 | | |AB| | |
| | 2sinαsinβsin(α + β)R2 | |
h = |
| = 2Rsinαsin(α + β) |
| | sinβR | |
17 kwi 01:02
Godzio:
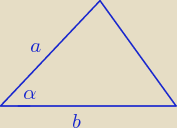
To jest wzór na pole
17 kwi 01:04
Sylwia: aha, nie wiedziałam, że jest taki wzór... Jesteś po studiach, że tak wszystko umiesz?
17 kwi 01:05
Ajtek: Godzio do matury się szykuje. Będzie zdawał podstawę, a za chwilę rozszerzenie

.
A tak to tylko na studia matematyczne sie wybiera

. Ot takie małe hobby
Godzia.
17 kwi 01:09
Godzio:
Ano

17 kwi 01:10
Sylwia: "Małe"... Ja też chce zdawać rozszerzenie z matmy

17 kwi 01:12
Ajtek: Godzio zobacz na tego robaczka
Ety może, co


.
17 kwi 01:12
Godzio:
Widziałem

i nie mam pojęcia jak to zrobić
17 kwi 01:13
Sylwia: no ta Eta to też ma łeb...
17 kwi 01:13
Godzio:
Jak na gimnazjalistkę to ma i to jaki

17 kwi 01:15
;): Godzio proszę Cię zrób je bo już nie wytrzymuje przy tym zadaniu z wielomianem

17 kwi 01:16
Godzio:
Które

?
17 kwi 01:16
Ajtek: Niestety swoich zeszytów z tamtych czasów juz nie mam

. A teraz jak znalazł by się przydał

17 kwi 01:16
;): Wyznaczyć tą wartość wielomianu dla W(0) i W(10) Znowu chyba pójdę spać po 3 przez to zadanie
17 kwi 01:22
Sylwia: Chce wam sie tak w nocy rozwiazywac zadania z matmy?
17 kwi 01:22
Ajtek: Chcę, czy też nie chcę, lubię. Nie zawsze mi to wychodzi, ale walczę

.
17 kwi 01:24
Sylwia: a Ty tez jestes teraz w klasie maturalnej?
17 kwi 01:27
Godzio:
Robię układ z 7 niewiadomymi i rozwiązuje : D
17 kwi 01:30
Ajtek: Nie, maturę zdawałem 13 lat temu

. I jakos się udało

.
17 kwi 01:30
Ajtek: Godzio ja zatrzymałem się na wyliczaniu b

Dalej nie brnąłem.
17 kwi 01:31
ICSP: całe forum na moim zadankiem siedzi

17 kwi 01:32
ICSP: nad*

17 kwi 01:32
Ajtek: ICSP złośliwcze (
szóstkowiczu), dawaj rozwiązanie. Pastwisz się nad nami

.
17 kwi 01:37
;): Widzisz coś narobił
ICSP heh

Słyszałem że masz 6 na koniec gratuluję

17 kwi 01:38
ICSP: Ja nie wiem jak to zrobić


17 kwi 01:38
ICSP: Jutro już eliminacją Gaussa się pobawię i rozwiąże ten układ równań

17 kwi 01:38
Ajtek: Jak widziesz, my też nie


17 kwi 01:39
Ajtek: A to w macierze będziesz wchodził

.
17 kwi 01:42
Godzio: −1,1069444444409x
6 + 23,262499999926x
5 − 193,92361111049x
4 + 815,43749999735x
3
−1805,4694444386x
2 + 1967,7999999936x −809,99999999737
W(0) = −809,99999999737
W(10) = −66171,9999998
W sumie banalne zadanie

17 kwi 01:42
Sylwia: No rzeczywiście, bardzo...
17 kwi 01:44
ICSP: hahahahahahahaha


17 kwi 01:45
Ajtek: Jak to wyliczyłeś

17 kwi 01:45
Godzio:
Mam swoje sposoby

17 kwi 01:45
ICSP: Mi to zadanie ciągle się z ciągami kojarzy

17 kwi 01:46
Sylwia: chcecie zadanie z dwoma gwiazdkami z mojej ksiazki? Tez z tego twierdzenia sinusów i cosinusów?
17 kwi 01:47
ICSP: Chyba jednak odpuśćże sobie eliminację Gaussa

17 kwi 01:47
Godzio:
Sylwia możesz dać

Mam nadzieję, że jakieś trudne będzie
17 kwi 01:47
Sylwia: dla mnie to kosmos, ale wy sobie na pewno dacie rade
17 kwi 01:48
ICSP: Myślę że teraz każde zadanie będzie banalnie łatwe

17 kwi 01:49
Ajtek: Hmmm, a atak na chłopski rozum dasz to radę przekształcić, tutaj masz wskazówkę
91790,
ostatni mój post.
ISCP mi też pod ciągi to podchodziło.
17 kwi 01:49
ICSP: Godzio pewnie do wolframka wpisał kolejne wyrazy ciągu a wolframek mu wzór ogólny ciągu
ułożył


17 kwi 01:50
Sylwia: | | s12+s22+s32 | |
Niech ABC bedzie dowolnym trojkątem .Oblicz stosunek |
| , gdzie |
| | a2+b2+c2 | |
a,b,c są dlugościami boków, a s
1, s
2, s
3 są dlugościami srodkowych tego trójkąta.
17 kwi 01:51
Godzio:
Wpisałem w programie współczynniki i mi wyliczył niewiadome

17 kwi 01:52
Godzio:
Robiłem już to zadanie, chyba korzystamy z tego samego zbioru Kłaczkowa

17 kwi 01:53
Sylwia: nooo... Mój zbiór zadań od matmy. Może sie jeszcze okaze, ze chodzimy do tej samej szkoły...
17 kwi 01:53
Godzio:
A jesteś z Wrocławia

?
17 kwi 01:55
Sylwia: nieee.... Z Warszawy.
17 kwi 01:56
Godzio:
No czyli nie chodzimy

17 kwi 01:57
Ajtek: No i "romansik" matematyczny nam się rysuje

. Niema to jak spam do zadania

17 kwi 01:57
Ajtek: No i po "romansie", a ja z bliskoch okolic Wawy jestem


17 kwi 01:58
Sylwia: e tam, od razu spam

17 kwi 01:58
Sylwia: bliskich, tzn?
17 kwi 01:58
17 kwi 01:58
Ajtek: A jednak spam

.
17 kwi 01:59
Ajtek: Bardzo bliskich, do centrum mam ≈22 km
17 kwi 02:00
Godzio:
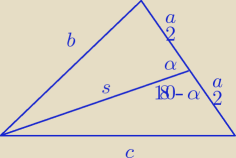
cos(180 − α) = −cosα
| | a2 | | a | |
s2 + |
| − 2s |
| cosα = b2 |
| | 4 | | 2 | |
| | a2 | | a | |
s2 + |
| + 2s |
| cosα = c2 + |
| | 4 | | 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
4s
2 = 2b
2 + 2c
2 − a
2
2s =
√2b2 + 2c2 − a2
Podstawiając długości poszczególnych środkowych otrzymujemy:
| 1 | |
| (2b2 + 2c2 − a2 + 2a2 + 2b2 − c2 + 2a2 + 2c2 − b2) | | 4 | |
| |
| = |
| a2 + b2 + c2 | |
17 kwi 02:01
Sylwia: moj brat który mieszka pod Wawa ma 20km. A napiszesz miejscowość? Może bede kojarzyc

17 kwi 02:01
Godzio:

17 kwi 02:02
Ajtek: Nie napiszę, ale dam wskazówkę:
Na wschód, związek z II RP.
17 kwi 02:03
Sylwia: Szybko to zrobiłeś

17 kwi 02:03
Sylwia: z II RP? Jestem cienka z historii...
17 kwi 02:04
Godzio:
Wiesz, jak się zna sporą ilość zadań na pamięć − patrzy się na zadanie i od razu wie się co
trzeba zrobić − to długo to nie zajmuje

Ale i tak najlepiej siedzieć nad tymi konkursowymi

17 kwi 02:05
Sylwia: jakas pierwsza litera?
17 kwi 02:05
Sylwia: Dobra, mam inne zadanie, nie ze zbioru.
17 kwi 02:07
Ajtek: Sylwia poszukaj w necie

.
17 kwi 02:07
Ajtek: Śmigam spać

. Pomyslcie nad tymi robaczkami
Ety 
. Spokojnych snów

17 kwi 02:08
Sylwia: Znajdź możliwie jak najmniejsza liczbę naturalną taką, że gdy jej skrajną prawą cyfrę
przesuniemy na jej lewy koniec − czyli, inaczej mówiąc, gdy jej ostatnią cyfrę przestawimy na
początek − to w ten sposób utworzona nowa liczba jest dokładnie 50% większa od początkowej
liczby. Wygrywa ten kto znajdzie najmniejsza taką liczbę.
17 kwi 02:09
Sylwia: robiłeś już to zadanie kiedys?

17 kwi 02:10
Godzio:
Jeszcze nie

Zaraz się zastanowię
17 kwi 02:13
Sylwia: Idę spać. Miłego myślenia.
17 kwi 02:27
Godzio:
Dzisiaj nie wymyślę, zasypiam już jutro się po zastanawiam

17 kwi 02:30

 Skąd tam się wzięło to d
Skąd tam się wzięło to d 
 |AC| = 2sinαR
|AB| = 2sinβR
|AC| = 2sinαR
|AB| = 2sinβR
 To jest wzór na pole
To jest wzór na pole
 .
A tak to tylko na studia matematyczne sie wybiera
.
A tak to tylko na studia matematyczne sie wybiera  . Ot takie małe hobby Godzia.
. Ot takie małe hobby Godzia.



 .
.
 i nie mam pojęcia jak to zrobić
i nie mam pojęcia jak to zrobić


 ?
?
 . A teraz jak znalazł by się przydał
. A teraz jak znalazł by się przydał
 .
.
 . I jakos się udało
. I jakos się udało  .
.
 Dalej nie brnąłem.
Dalej nie brnąłem.


 .
.
 Słyszałem że masz 6 na koniec gratuluję
Słyszałem że masz 6 na koniec gratuluję





 .
.







 Mam nadzieję, że jakieś trudne będzie
Mam nadzieję, że jakieś trudne będzie





 ?
?

 . Niema to jak spam do zadania
. Niema to jak spam do zadania 




 A jesteś z Wrocławia?
nie.... z Warszawy
No czyli nie chodzimy
A jesteś z Wrocławia?
nie.... z Warszawy
No czyli nie chodzimy

 .
.
 cos(180 − α) = −cosα
cos(180 − α) = −cosα



 Ale i tak najlepiej siedzieć nad tymi konkursowymi
Ale i tak najlepiej siedzieć nad tymi konkursowymi

 .
.
 . Pomyslcie nad tymi robaczkami Ety
. Pomyslcie nad tymi robaczkami Ety  . Spokojnych snów
. Spokojnych snów

 Zaraz się zastanowię
Zaraz się zastanowię
