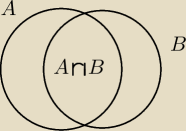prawdopodobieństwo Ziomal: zdarzenia A i B zawierają się w przestrzeni zdarzeń elementarnych Ω, a P jest prawdopodobieństwem określonym w tej przestrzeni . wiedząc że:

	1		1
P(A\B)=P(B\A) ; P(A∪B)=		; P(A∩B)=
	2		4

Oblicz: P(B) i P(A'∩B)

	3
nie wiem jak policzyć P(B) W odpowiedziach w zbiorze mam że ma wyjść		pomoże ktoś?
	8

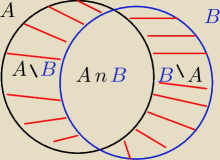zajączek: P(A \ B)= P(B \A)= 2P(A \ B)

	1
P(A U B)= 2*P(A\ B)+ P(A ∩ B) => ....... P(A \ B)=		= P(B \ A)
	8

	3
P(B) = P(B \A) + P(A ∩ B) => ........... P(B) =
	8

P(A^' ∩ B) = P(B \ A)=P(A \B) =........

Ziomal: Dzięki