 3√x = 4 − x2 ⇒ x = 1
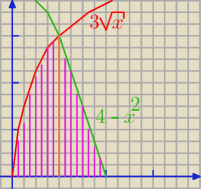
Masz tu sumę dwóch obszarów, jeden znajduje się od 0 do 1 (pomiędzy krzywymi y = 3√x i y = 0)
a drugi od 1 do 2 (pomiędzy y = 4 − x2, a y = 0)
Jak widać na rysunku w pierwszym przedziale y = 3√x leży ponad y = 0 więc zapisujemy całkę:
01∫(3√x − 0)dx
Drugi obszar, y = 4 − x2 leży ponad y = 0 więc:
12∫(4 − x2 − 0)dx
01∫3√xdx + 12∫(4 − x2)dx = ... Teraz licz
3√x = 4 − x2 ⇒ x = 1
Masz tu sumę dwóch obszarów, jeden znajduje się od 0 do 1 (pomiędzy krzywymi y = 3√x i y = 0)
a drugi od 1 do 2 (pomiędzy y = 4 − x2, a y = 0)
Jak widać na rysunku w pierwszym przedziale y = 3√x leży ponad y = 0 więc zapisujemy całkę:
01∫(3√x − 0)dx
Drugi obszar, y = 4 − x2 leży ponad y = 0 więc:
12∫(4 − x2 − 0)dx
01∫3√xdx + 12∫(4 − x2)dx = ... Teraz licz
| 11 | |
powinno chyba wyjść | |
| 3 |
| x3/2 | 2 | 2 | ||||||||||
10∫3√xdx = 3 * | |10 = 3 * | * 13/2 − 3 * | * 03/2 = 2 | |||||||||
| 3 | 3 |
| x3 | 8 | 1 | 7 | 5 | ||||||
21∫(4 − x2)dx = 4x − | |21 = 8 − | − 4 + | = 4 − | = | ||||||
| 3 | 3 | 3 | 3 | 3 |
| 5 | 11 | |||
więc: 2 + | = | |||
| 3 | 3 |
