w zależności od parametru m dd: Naszkicuj wykres funkcji |x²−4|. Następnie korzystając z wykresu funkcji, określ liczbę rozwiązań równania |x²−4|=m w zależności od parametru m

Rivi: Narysuj normalny wykres x²−4, a to co będzie poniżej OX "odbij" do góry. Wtedy odczytać będzie prosto

dd: nie wiem jak odczytać, daj mi proste wskazówki , mam coś takiego w rozwiązaniu: 0 dla m nalezącego do (−nieskończoność;0) − co to znaczy?

Ajtek: Jedziesz od dołu po osi OY i patrzysz ile ma rozwiązań. Najlepiej zrobić to przy pomocy linijki.

dd: nie czaję; przy zerze mam miejsca zerowe −2 i 2, a nie to co wskazałem; przy jedynce to mam... nie czaję tego

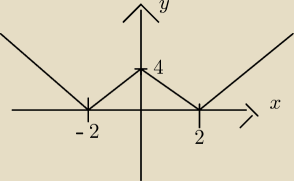
Rivi: m to jest tak jakby "y" masz taki wykres (tylko parabole oczywiście) i widzisz, że od −∞ do zera nie ma żadnych rozwiązań gdy m=0 (czyli oś OX) są dwa rozwiązania (−2 i 2) od (0,4) masz cztery rozwiązania (ile iksów ma taką wartość) gdy m=4 masz 3 rozwiązania i od 4 do +∞ masz dwa rozw.