Zadania z parametrem. Bardzo proszę o pomoc! hidden_puma: Witajcie Siedzę nad tymi zadaniami i siedzę i coś tam dziubnęłam, ale nie mogę nic dokończyć Pomożecie? 1. Wyznacz takie wartości m, dla których pierwiastki rzeczywiste x₁ i x₂ równania 2x²−(m+3)x+(m²−5)=0 spełniają warunek x₁<1<x₂ 2.Dla jakiej wartości parametru m równanie x²−2|x|−2=m ma trzy rozwiązania? Znajdź te rozwiązania. 3. Niech f będzie funkcją, która każdej liczbie rzeczywistej m przyporządkowuje liczbę pierwiastków rzeczywistych równania (x²−1−m)(|x|−1−m)=0. Sporządź wykres funkcji f. 4. Dla jakich wartości rzeczywistych parametru m równanie x² −mx+2m−3=0 ma dwa różne rozwiązania rzeczywiste należące do przedziału (−1;5)? 5. Wyznacz zbiór tych wszystkich wartości parametru k, dla których dziedziną funkcji

	1
f(x)=		jest zbiór licz rzeczywistych?
	/√x2−4kx+12k−4k2

6. Dla jakich wartości parametru m równanie (m−1)x⁴−2(m+4)x²+m=0 ma dokładnie dwa rozwiązania? 7. Wyznacz te wartości parametru rzeczywistego m, dla których równanie (x²−2x+m−2)(|x−1|−m+1)=0 ma dokładnie trzy pierwiastki rzeczywiste. Oblicz te pierwiastki. Bardzo, ale to bardzo proszę o pomoc, bo zadania z parametrem to dla mnie nowość, a nie miałam tego w szkole i jestem zielona. Jeśli można to byłabym wdzięczna za w miarę logiczne wytłumaczenie rozwiązań tych zadań.

Maryjusz: 2. f(x)={x²−2x−2, dla x≥0 {x²+2x−2, dla x<0 Narysuj wykres tej funkcji i odczytaj w jakich przedziałach ma 3 rozwiązania. 5. x²−4kx+12k−4k²>0 6. Δ≥0

Maryjusz: w 5 jeszcze robisz, że x²=t, t>0 wtedy masz równanie kwadratowe

Maryjusz: w 6. sorki

hidden_puma: Srednio mi to pomogło, ale zawsze coś, dzięki. Chociaż przydałoby mi się gdyby ktoś mi krok po kroku przeanalizował te zadania...

hidden_puma: Hej, jeszcze raz bardzo proszę o pomoc. W zadaniu 1 chyba powinnam policzyć Δ>0, ale za Chiny mi nie chce wyjść Δ. No bo chyba powinno być: (−m−3)²−4*2*(m²−5)>0 m²−6m+9−8m²+40>0 −7m²−6m+49>0 Δm=36−4*(−7)*49 Δm=36+1372=1408 No i nie mam żadnego sensownego pierwiastka z tego i co dalej? A co do warunku, to ma być z Viete'a? np. x₁+x₂∊(−∞;1)∪(1;∞) a potem będzie −∪{b}{a}>1 i −∪{b}{a}<1 ?

hidden_puma: tam po x1+x2 zle mi sie dzieleni zrobiło, ale wiadomo o co chodzi.

Pat: 1. Wyznacz takie wartości m, dla których pierwiastki rzeczywiste x1 i x2 równania 2x2−(m+3)x+(m2−5)=0 spełniają warunek x1<1<x2 f(x)=2x2−(m+3)x+(m2−5) Żeby funkcja f(x) miała dwa różne pierwiastki x1 i x2, Δ>0 Δ=m²+6m+9−8m²+40 Δ=−7m²+6m+49 Δ>0⇒−7m²+6m+49>0 Δm=36+1372=1408 √Δm=8√22

	3+4√22
m1=
	7

	3−4√22
m2=
	7

Dziedzina Δ, mówi że m∊(m2,m1) Wyznaczam pierwiastki f(x):

	7m2−5m−36
x1=
	4

	−7m2+7m+52
x2=
	4

x1<1<x2

7m2−5m−36		−7m2+7m+52
	<1<		/*4
4		4

7m²−5m−36<4<−7m²+7m+52 Co sprowadza się do: 7m²−5m−36<4 i 7m²−5m−36<−7m²+7m+52 i −7m²+7m+52>4 Trzeba rozwiązać 3 nierówności, wyciągnąć część wspólną, bo spójnik "i", i sprawdzić z dziedziną. Jeżeli nie popełniłem żadnego błędu rachunkowego ani z założeń to powinno być dobrze. Nie wiem czy wzory Viete'a są tu potrzebne, ale mogę się mylić.

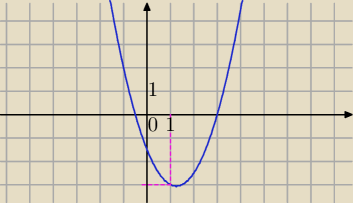
Mila: Wyznacz takie wartości m, dla których pierwiastki rzeczywiste x1 i x2 równania 2x²−(m+3)x+(m²−5)=0 spełniają warunek x₁<1<x₂ Wykres ma być tego typu co narysowałam: Warunki: 1) Δ>0 dwa rozwiązania 2) f(1)<0 =========== 1) Δ=(m+3)²−4*2*(m²−5)=−7m²+6m+49

	3−4√22		3+4√22
Δ>0⇔m∊(		,		)
	7		7

2) f(1)=2−(m+3)+m²−5<0⇔ m∊(−2,3)

	3−4√22		3+4√22
Cześć wspólna przedziałów: (−2,3)∩(		,		)=(−2,3)
	7		7

m∊(−2,3) Czy taka jest odpowiedź?

Blee: Miluś −−− to jest 10 miesięczny odkop

Szkolniak: Dziesięcioletni

ABC: dobry odkop nie jest zły

Pat: Czyli ten mój sposób jest nie do końca dobry? Rozumiem dlaczego 2) założenie Mili o f(1)<0, ale czy moje założenie jest niepoprawne? Tj. wyznaczenie wzorów pierwiastków i zapisanie nierówności x1<1<x2?

Mila: To napisz wzory rozwiązania równania kwadratowego i porównaj z tym co napisałeś. Zakładaj nowe wątki , nie odkopuj starych , bo to jest mylące

Mila: Można tak : x₁<1<x₂ ale trzeba dobrze napisać wzory. Chyba będzie trudniej.

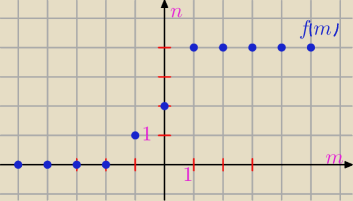
Pat: 3. Niech f będzie funkcją, która każdej liczbie rzeczywistej m przyporządkowuje liczbę pierwiastków rzeczywistych równania (x2−1−m)(|x|−1−m)=0. Sporządź wykres funkcji f. Niech n_m oznacza ilość pierwiastków równania (1) w zależności od m (1) (x²−1−m)(|x|−1−m)=0 dla m = −3: (x²+2)(|x|+2)=0 n₋₃=0 dla m = −2: (x²+1)(|x|+1)=0 n₋₂=0 dla m = −1: x²|x|=0 n₋₁=1 dla m = 0: (x²−1)(|x|−1)=0 n₀=2 dla m = 1: (x²−2)(|x|−2)=0 n₁=4 dla m = 2: (x²−3)(|x|−3)=0 n₂=4 dla m = 3: (x²−4)(|x|−4)=0 n₃=4 gdy m ≤ 2 ⇒ n_m=0 gdy m = −1 ⇒ n_m=1 gdy m = 0 ⇒ n_m=2 gdy m ≥ 1 ⇒ n_m=4 Wykres wyżej. Ja bym to tak rozwiązał na maturze, ale nie jestem pewny. Nie jest to najszybsze rozwiązanie, ale rachunkowo sobie tego nie wyobrażam. Dłużej rysowałem ten wykres

Pat: 4. Dla jakich wartości rzeczywistych parametru m równanie x2 −mx+2m−3=0 ma dwa różne rozwiązania rzeczywiste należące do przedziału (−1;5)? f(x)=x²−mx+2m−3 Założenia

⎧	Δ>0 bo dwa różne pierwiastki
⎨	f(−1)≥0
⎩	f(5)≥0

Δ=m²−8m+12 Δ>0 ⇒ m²−8m+12 > 0 Δ_m = 64−48 = 16 √Δ_m=4 m₁ = 2 m₁ = 6 m ∊ (−∞,2)u(6,∞) f(−1)=3m−2 f(−1) ⇒ 3m≥2 m ≥ ²₃ f(5)=−3m+22 f(5) ⇒ −3m≥−22 m ≤ ²²₃

⎧	m ∊ (−∞,2)u(6,∞)
⎨	m ≥ 23
⎩	m ≤ 223

Odpowiedź: m ∊ <²₃,2)u(6, ²²₃> Prosiłbym o odpowiedzi do zadań, bo to też dla mnie sygnał, że dobrze rozumuję

Pat: W 3. źle zrobiłem wykres, bo jest powiedziane, że dla każdego m ∊ R, a ja zrobiłem dla m ∊ Z. Chyba tą moją metodą nie wyjdzie.

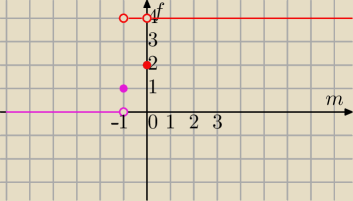
Mila: (x²−1−m)(|x|−1−m)=0⇔ (x²−1−m)=0 lub (|x|−1−m)=0 ⇔ 1) (*) x²=m+1 (x²≥0 dl x∊R) a)m+1=0⇔m=−1 jedno rozwiązanie (x=0) m+1>0⇔m>−1 dwa rozwiązania [ x=√m+1 lub x=−√m+1]] m<−1 0 rozwiązań lub 2)(**) |x|=m+1 (|x|≥0 dla x∊R) m+1=0 ⇔m=−1 jedno rozwiązanie (x=0) m+1>0⇔m>−1 dwa rozwiązania m<−1 0 rozwiązań ====================== 3) ponieważ x²=m+1 i |x|=m+1 to sprawdzamy kiedy x²=|x| x=0 lub x=1 lub x=−1 czyli dla m+1=0 lub m+1=−1 lub m+1=1 ⇔ dla m=−1 lub m=−2 lub m=0 równania mają wspólne rozwiązania przy czym dla m<−1 obydwa równania nie mają rozwiązań ================================== f(m)=0 dla m<−1 (brak rozwiązań) f(−1)=1 czyli dla m=−1 jedno rozwiązanie f(m)=4 dla m∊(−1,0) cztery rozwiązania f(0)=2 dla m=0 dwa rozwiązania f(m)=4 dla m>0 ====================

Mila: Załóż nowy wątek, bo trzeba długo przewijać stronę

Pat: 5. x²−4kx+12k−4k²>0 f(x) = x²−4kx+12k−4k² Skoro współczynnik przy najwyższej potędze jest dodatni to ramiona funkcji będą skierowane do góry. Żeby zbiorem rozwiązań x były wszystkie liczby rzeczywiste to Δ musi być mniejsza od 0. Wtedy f(x) nie będzie miało pierwiastków i wykres będzie powyżej osi OX. Δ=32k²−48k Δ<0 ⇒ 32k²−48k<0 k(32k−48)k<0 k=0 lub k=⁴⁸₃₂=³₂ k∊(0,³₂) □