parametr RunLikeHell: Dla jakich wartości parametru p, gdzie p∊R równanie h(x)=p²−1 ma dwa rozwiązania różnych znaków?

	2
h(x)=|−		−3|
	x+1

RunLikeHell: refresh

Godzio: Narysuj ten wykres i wyznacz przedział w którym dowolna prosta y = p² − 1 ma 2 punkty wspólne z wykresem i przecina go w x ujemnych i dodatnich

RunLikeHell: to jest prosta czy parabola?

Artur:

	2
h(x)=		potem przesuń raz w lewo 3 razy w dół i odbij to co jest na dole.
	x

y=p²−1 to parabola o 1 przesunięta w dół, której osią symetri jest oś OY.

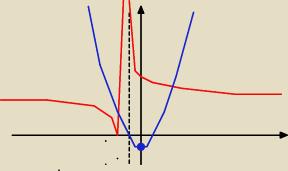
Artur: ale jak sobie to tak narysowałem. to nie wiem czy o to chodziło Gondzio

RunLikeHell: Dokładnie tak to sobie tez wyobrażałem, z tym, że jak z tego odczytać przedziały? I jak zmieni się parabola wraz ze zmianą p ? poprostu ramiona będą się zawężały albo rozszerzały? odp do zadania to : p∊(−√6;−2)U(2;√6)

RunLikeHell: 123

RunLikeHell: odświeżam

RunLikeHell: i znowu

Deryl: Dokładnie tak.

RunLikeHell: no ok, to teraz jak te przedziały odczytać ?

Deryl: Podkładasz 0,1,2,3 i robisz tabelkę. Przynajmniej z tego co pamiętam Głowy sobie nie dam uciąć

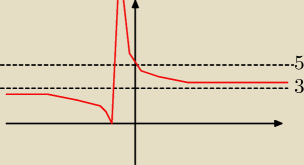
Artur: y=p²−1 w tym przypadku będzie prostą, widać na Osi OY ze dwa rozwiązania o różnych znakach rozdzielają proste(asymptoty) y=3 i y=5 z twojej odpowiedzi po podstawieniu p∊(−√6;−2)U(2;√6), wynik zawsze będzie między tymi prostymi inna możliwość: p²−1>3 => dla p> 2 lub p> −2 p²−1<5 => dla p< √6 lub p<√6

rrrr: nie jestem pewien ale wydaje mi się że takie zadani można rozwiązywać wykorazystując wzory vietea zna różnorodność i znaki rozwiązań regulują znaki przy iloczynie i sumie rozwiązań

RunLikeHell: dzięki za odp byłbym wdzięczny jakby ktoś to jeszcze zweryfikował