Funkcja kwadratowa Kamila: Prosze o pomoc...Dana jest funkcja kwadratowa f(x)=¹₄x²+x−8, x∊R. a. Wyznacz miejsce zerowe funkcji. b. Rozwiąż nierownosc f(x)>−8 c. Wyznacz najwieksza oraz najmniejsza wartosc funkcji na przedziale <1,3>

magda: a) skoro masz wyznaczyć miejsca zerowe to musisz zawsze za f(x) podstawić 0 i wyliczyć x, czyli

	1
f(x)=		x2+x−8
	4

	1
0=		x2+x−8
	4

	1
a=		b=1 c=−8
	4

	1
Δ=b2−4ac=1−4*		*(−8)=1+8=9
	4

√Δ=√9=3

	−b−√Δ		−1−3
x1=		=		=−8
	2a		2*14

	−b+√Δ		−1+3
x2=		=		=4
	2a		2*14

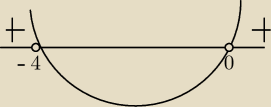
magda: b) f(x)>−8

	1
f(x)=		x2+x−8
	4

1
	x2+x−8>−8
4

1
	x2+x−8+8>0
4

1
	x2+x>0
4

	1
x(		x+1)>0
	4

	1
x(		x+1)=0
	4

	1
x=0 lub		x+1=0
	4

	1
		x=−1 \4
	4

x=−4 x∊(−∞,−4)∪(0,∞)

Karina: miejsce zerowe ustalamy w następujący sposób obliczamy Δ=b²−4ac=1²−4*1/4*(−8)=9 i √Δ=3wzory na miejsca zerowe następujące x₁= −b−√Δ/2a i x₂= −b +√Δ stad x₁= −2 a x₂=8 nierówność rozwiązujemy tak 1/4x²+x−8> −8 →1/4x²+x>0 x(1/4x+1)>0 x=0 lub x= −4 rozwiązuje na osi liczbowej gałązki funkcji do góry stąd rozwiązaniem są przedziały (−∞;−4)∪(0;+∞) najmiejszą wartośc przyjmuje wierzchoek czyli (p;q) →p=−b/2a →p=−2 a q=f(p)=−10

magda: <1,3> mamy tu liczby 1 oraz 3 teraz musimy do wzoru funkcji podstawić 1

	1		1		1
f(1)=		12+1−8=		+1−8=1		−8=−6{3}{4}
	4		4		4

a teraz podstawiamy 3

	1		9		1		1
f(3)=		33+3−8=		+3−8=2		+3−8=5		−8=−2{3}{4}
	4		4		4		4

teraz należy wyliczyć "p"

	−b
p=
	2a

	−1
p=
	2*14

	−1
p=
	12

p=−2

	1
f(−2)=		(−2)+(−2)−8=1−2−8=−9
	4

	3		3
teraz spośród liczb −6		−2		−9 wybieramy największą i najmniejszą
	4		4

zatem

	3
największa wartość funkcji to −2
	4

a najmniejsza wartość to −9

ICSP: magda sprawdź tok rozumowania w ostatnim.

Kamila: dzieki wielkkie*

ICSP: czekaj Kamilu jeszcze magda sprawdzi ostatni podpunkt i coś stwierdzi

ICSP: no i magda poszła:( x_w nie należy do rozpatrywanego przedziału. Dlatego odpowiedzi:

	3
najmniejsza wartość to −6
	4

	3
największa wartość −2
	4

Kamila: ICSP jestem dziewczyną