zad Ulf: Wykaż że równanie ma dokładnie jeden pierwiastek. x³−3x+3=0

Ulf: proszę o poradę, bo stoję

Bizon: wiesz jak wygląda wykres funkcji y=x³ ...?

Ulf: wiem, wiem tez ze trzeba uzyc pochodnej

Bizon: nałóż na niego wykres y=3x−3

Jack: Proponuję tak: policz ekstrema i pierwiastki funkcji f(x)=x³−3x. Potem podnieś tę funkcję o 3 jednostki w górę i przeanalizuj liczbę pierwiastków.

Bizon: nie trzeba tu żadnej pochodnej Wystarczy tabelka. Nikt Cię nawet nie pyta o ten pierwiastek ... tylko o wykazanie ze jest jeden.

Ulf: rzeczywiście z postaci: x(x−√3)*(x+√3) widać pierwiastki, ale co z tego skoro nie mam wierzchołków, co przy przesuwaniu o wektor [0;3] ma różnicę; co z tą tableką i czy będzie ona rzeczywiście wykazaniem

Jack: tabelka służyła dzieciom w gimnazjum, żeby w ten sposób "wykazywać" istnienie bądź nieistnienie czegoś... Sama tabelka nie wystarczy na pewno, z chęcią przeczytam Twoją propozycję rozwiązania, Bizon.

Jack: jesli myślisz o mojej metodzie, to zauważ, że napisałem o EKSTREMACH tej funkcji.

Ulf: y=x³−3x y`=3x²−3 wykresem jest parabola z ramionami do góry, z miejscami zerowymi −1 i 1, z wierzcholkiem w P=(0;−3), wiec jak podniesiemy o 3 do gory to bedzie jedno miejsce zerowe w punkcie (0;0), tak?

Jack: estrema to 1 i −1. Teraz wartość funkcji y=f(x)=x³−3x w tych punktach. f(1)=−2 f(−1)=2 ponadto pierwiastki f(x) w x=0,√3,−√3. Łatwo taką funkcję narysować... Więc teraz jak przesuniesz cały wykres f(x) w górę o 3 jednostki, to ektremum nie sięgnie osi OX, i pozostanie jeden pierwiastek

Ulf: Ekstrema rozumiem, ale po słowie "podanto" nie rozumiem

Bizon: Do Jack : rozprawki naukowe to będziesz pisał jak już zdasz maturę. Krzywa y=x³ jest najprostszą z krzywych trzeciego stopnia. Jej wykres jest banalny. Nic też prostszego jak pokazać, że ma on tylko jeden punkt wspólny z prostą y=3x−3. I o nic więcej w tym zadaniu nie pytają.

ICSP: x³ = 3x − 3 Nie prościej narysować te dwa wykresy i wypadnie ze przetną się w tylko jednym miejscu?

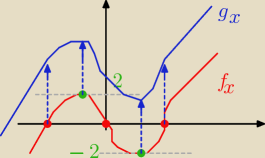
Jack: Oznaczenia: g(x)=x³−3x+3 f(x)=x³−3x=x(x−√3)(x+√3) Stąd będziemy mieli że g(x)=f(x)+3 f'(x)=3x²−3=3(x²−1)=3(x−1)(x+1) Widać, że ekstrema f(x) to x=1, x=−1 (można szybko sprawdzić warunek wystarczający). Wartość funkcji f w tych punktacj to odpowiednio: f(1)=−2, f(−1)=2 Mam nadzieję żę rys. są czytelne... Kluczowe punkty dla analizy funkcji g(x) to ekstrema funkcji f(x).

Bizon: Jeśli zaś sądzisz, że łatwiej narysować y=x³−3x niżeli y=x³ ... to gratuluję ...

Jack: Tak wiec pokazałeś fajną metodę, i to mi chodziło. Wspomnienie "tabelki" wywołało we mnie taką reakcję.

Jack: Tak wiec pokazałeś fajną metodę, i to mi chodziło. Wspomnienie "tabelki" wywołało we mnie taką reakcję.

Bizon: Najlepszym dowodem, że się zaplątałeś są te przekształcenia i przybliżone miejsce pierwiastka