ktore rozwiązanie jest poprawne ?
Werutka: x
3 − 9x = 6x
x
3 − 9x = 6x
2 | − 6x
2
x
3 − 9x − 6x
2 = 0
x (x
2 − 6x − 9) =0
Δ wychodzi =0
Xo = 3
x
3 − 9x = 6x
2 | − 6x
2
x
3 − 6x
2 − 9x =0
x (x
2 − 6x −9) =0
x (x − 3)
2 =0
x(x
2 − 9) =0
x (x − 3) (x + 3) =0
x= 0, x1=3, x2= −3 −ten przykład robiła koleżanka, mi wyszło inaczej, jeżeli ten jest dobry
proszę o wytłumaczenie skąd taki kosmos

14 kwi 18:10
Kejt: Δ nie wychodzi zero.. 36+4*9=...
14 kwi 18:21
Werutka: tak masz rację, przeoczyłam znak

ale które rozwiązanie jest poprawne ?

14 kwi 18:26
Werutka: nie patrząc na moją złą delte
14 kwi 18:27
Kejt: Twojej koleżanki jest złe x2−9≠x2−6x−9.
14 kwi 18:30
Kejt: i dodatkowo: (x−3)2≠x2−9
14 kwi 18:31
Ola: x3−6x2−9x=0
x(x2−6x−9)=0
Δ=36−4(−9)=36+36=72
√Δ=6√2
x(x−3+3√2)(x−3−3√2)
x1=0 v x2=3−3√2 v x3=3+3√2
14 kwi 18:34
Werutka: masło maślane, ale dzięki
14 kwi 18:54
ko: x
3 − 6x
2 − 9x = 0
x(x
2 − 6x − 9) = 0
x = 0 v x
2 − 6x − 9 = 0
Δ = 36 + 36 = 72 = 6
√2
| | 6−6√2 | | 6+6√2 | |
x = |
| v x = |
| |
| | 2 | | 2 | |
| | 6(1−√2) | | 6(1+√2) | |
x = |
| v x = |
| |
| | 2 | | 2 | |
x=0 x = 3(1−
√2) v x = 3(1+
√2)
x ∊ { 3(1−
√2) , 0 , 3{1+
√2 }
14 kwi 19:02
ukasz: 
14 kwi 19:07
Werutka: 2x3 − x2 + 18x − 9= 0
14 kwi 19:18
ukasz: x
2 (2x − 1) + 9 (2x − 1) = 0
(2x−1)(x
2+9)=0
| | 1 | |
(x− |
| ) = 0 v (x2+9) = 0 |
| | 2 | |
| | 1 | |
x = |
| równanie sprzeczne |
| | 2 | |
14 kwi 19:21
Werutka: 2x
3 − x
2 − 6x + 3 =0
x
2 (2x −1) 3(2x + 1) =0
(2x−1) (x
2 + 3) =0
14 kwi 19:37
ukasz: 2x
3 − x
2 − 6x + 3 = 0
x
2(2x − 1) − 3 (2x−1) = 0 − nawiasy muszą byc takie same!
(2x−1)(x
2 − 3) = 0 a
2 − b
2 = (a+b)(a−b)
| | 1 | |
2(x− |
| ))(x+√3)(x−√3) = 0 |
| | 2 | |
| | 1 | |
x− |
| = 0 v x+√3 = 0 v x−√3 = 0 |
| | 2 | |
14 kwi 19:42
Werutka: wskaż równanie osi symetrii paraboli określonej równaniem y= x
2 − 2x + 3 odpowiedź uzasadnij

a x=3, b x= −1 c x= 1 d x=3
14 kwi 20:15
ukasz: y=x
2 − 2x + 3
| | −b | |
W(p, q) p= |
| W − wierzchołek paraboli  |
| | 2a | |
Czyli oś symetrii paraboli to x = 1

14 kwi 20:23
ukasz:
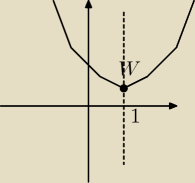
Tak to mniej− więcej wygląda

14 kwi 20:25
Werutka: rozwiąż nierówność (x + 1) (x − 3) >0
14 kwi 20:36
ukasz: Ona jest już rozwiązana

Odczytujesz miejsca zerowe.
czyli x+1 = 0 , x−3=0 (ale to w pamięci)
czyli x= −1 i x = 3
Robimy rysunek:
14 kwi 20:38
ukasz:
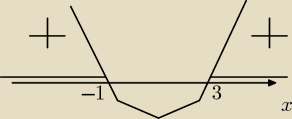
Szukamy wartości > 0. czyli Wszystko co jest ponad osią X zakreskowywujemy

czyli x∊(−
∞;−1) u (3;+
∞)
Powinno to wyglądać tak:
(x+1)(x−3)>0
(rysunek)
(x∊())
14 kwi 20:40
ukasz: Gdyby było to samo, tylko, że (x+1)(x−3)< 0
to robimy tak samo, tylko, że zaznaczamy to poniżej osi x
wychodzi, ze x∊(−1;3)
14 kwi 20:42
Werutka: podaj zbiór wartości oraz współrzędne wierzchołka funkcji o równaniu
a) f(x) = −(x+2)2 − 3
b) f(x) = 2x2 −1
14 kwi 20:51
ukasz: a)
f(x) = −(x+2)2 − 3
W(p,q) − współrzedne wierzchołka
f(x) = a(x−p) + q − postać kanoniczna
Więc wierzchołek W (−2, −3).
Współczynnik a jest ujemny, więc ramiona paraboli skierowane są w dół.
Zatem zbiorem wartości funkcji jest przedział (−∞;−3>.
14 kwi 20:53
ukasz:
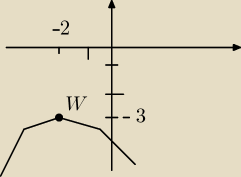
Tak to wygląda

14 kwi 20:55
ukasz: b)
f(x) = 2x2 − 1
to to samo co:
f(x) = 2(x + 0)2 − 1
Czyli W(0, −1)
Współczynnik jest dodatni, zatem ramiona skierowane są ku górze
Zbiorem wartości funkcji jest przedział (−1; +∞)
14 kwi 21:07
ukasz:
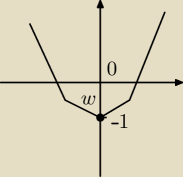
14 kwi 21:08

 ale które rozwiązanie jest poprawne ?
ale które rozwiązanie jest poprawne ?

 a x=3, b x= −1 c x= 1 d x=3
a x=3, b x= −1 c x= 1 d x=3


 Tak to mniej− więcej wygląda
Tak to mniej− więcej wygląda 
 Odczytujesz miejsca zerowe.
czyli x+1 = 0 , x−3=0 (ale to w pamięci)
czyli x= −1 i x = 3
Robimy rysunek:
Odczytujesz miejsca zerowe.
czyli x+1 = 0 , x−3=0 (ale to w pamięci)
czyli x= −1 i x = 3
Robimy rysunek:
 Szukamy wartości > 0. czyli Wszystko co jest ponad osią X zakreskowywujemy
Szukamy wartości > 0. czyli Wszystko co jest ponad osią X zakreskowywujemy  czyli x∊(−∞;−1) u (3;+∞)
Powinno to wyglądać tak:
(x+1)(x−3)>0
(rysunek)
(x∊())
czyli x∊(−∞;−1) u (3;+∞)
Powinno to wyglądać tak:
(x+1)(x−3)>0
(rysunek)
(x∊())
 Tak to wygląda
Tak to wygląda 
