funkcja liniowa Nowa: Dane są równania trzech boków trójkąta: 2x−y=0 x+y+3=0 x−2y+3=0 Napisz równania prostych zawierających wysokości tego trójkąta.

Nowa: pomoże ktoś?

cvb: hej Nowa ja tez tu jestem prawie nowy , a tak dokladnie to wczorajszy dlatego nie oblicze Ci tego tylko napisze co nalezy zrobic ; a wiec tak : 1. porównaj 2 proste do siebie i wyznacz punkt ich przeciecia −np.A, nastepnie wiedzac ze prosta zawierajaca wysokos jest prostopadła do naszej trzeciej prostej tak wiec współczynik (a) jest odwrotny i przeciwny i wiemy rowniez ze ta prosta przechodzi przez punkt A(..,...) no i mamy jedna prosta zrobiona , to samo robisz z pozstałymi

Nowa: próbowałam tak zrobić, lecz nie chciało mi wyjść... narysowałam nawet taki rysunek pomocniczy opisałam jego boki tymi równaniami, wyliczyłam punkty przecięcia i potem standardowo liczyłam proste prostopadłe, ale nie wyszło

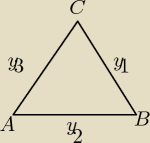
cvb: y₁=−x−3, y₂=1/2x + 2/3 , y₃=2x y=2x y=1/2x + 3/2 − uklad rownan x_A=1 y_A=2 Nastepnie towrzymy prosta prostopadła do prostej y₁ y=x+b , ktora przechodzi przez punkt A=(1,2) 2=1+b→b=1 czyli y=x+1

Nowa: a dlaczego podstawiasz do równania y=x+b, a nie do y=ax+ b?

Nowa: zrobiłam tym twoim sposobem i nie wyszło tak jak ma wyjść...

cvb: poniewaz a jest odwrotne i przeciwne do −1 , co z tego wynika ze nasze a =1 , czyli y=x+b

Nowa: jak już napisałam zastosowałam to do reszty i nie działa...

cvb: ok wiec zajmiemy sie teraz punktem B , y=−x−3 y=1/2x+3/2 − odejmuje stronami o=−3/2x−9/2 − mnoze razy 2 0=−3x−9→x=−3,y=0 →B=(−3,0) teraz szukamy prostej prostopadłej do prostej y=2x czyli współczynnik a bedzie odwrotny i przeciwny do 2 czyli nasz a=−1/2 y=−1/2x+b wiemy ze ta prosta przechodzi przez punkt B=(−3,0) 0=3/2+b →b=−3/2 prosta ktora wyliczylismy ma postac y=−1/2x−3/2