PROblem TOmek:

	3		4
Dana są zdarzenia A, B ⊂ Ω takie ,ze P(B)=		, P(A u B)=		. Oblicz prawdopodobieństwo
	7		5

zdarzenia A \ B. Najwazniejsze jest by udowodnić ,ze A i B są rozlączone ,tylko jak?

Godzio: Ale na co ty chcesz udowodniać to że one są rozłączne ?

TOmek: bo pierw trzeba to udowodnic ,by mozna było skorzystac z tego wzorku P(A u B)=P(A)+P(B), chyba ,ze jest to oczywiste ,ze są rozłączone ale ja tego nie widze

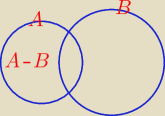
Godzio: A kto Ci karze korzystać z tego wzorku ? P(AUB) − P(B) = P(A − B)

4		3
	−		= P(A − B)
5		7

	28 − 15		13
P(A − B) =		=
	35		35

TOmek: akurat w tym zadaniu trzeba uzyc prawo De Morga, ale bardziej mnie obchodzi o to skąd mam wiedziec czy A i B są rozlączne?xD

TOmek: no wynik dobry xD tylko ciekawi mnie czy za takie rozwiązanie byś miał max. pkt. jeśli ja mam w odp. tak: 1 pkt. zapisane działan : A u B = (A \ B) u B ⋀ (A \ B) n B = ∅ 2.wykorzstanie aksomatu do zapisania prawo....: P(A u B)=P(A \ B) + P(B) 3.wynik ... I ciekawi mnie czy bym miał max. pkt. rozwiązaując Twoim sposobem

Godzio: Moim zdaniem narysowanie takiego grafu, zaznaczenie szukanego obszaru, zapisanie P(A − B) = P(AUB) − P(B) i rozwiązanie dostało by się maxa

TOmek: ok to biore sie juz za permutacje, wariacje i inne dziwne słowa xD

TOmek: a takie pytanko P(A \ B)= P(A) − P(B) poprawny jest taki zapis?

Godzio: Nie

Eta: P(A U B) = P(A)+P(B) − P(A ∩ B)

4		3
	= P(A) +		−P(A ∩ B)
5		7

	4		3
P(A) − P(A ∩ B)=		−		= ........... = P(A \ B)
	5		7

Vizer: Nie jest poprawny przerzuć sobie P(B) na drugą stronę i masz tak: P(A)=P(A/B)+P(B) a to się nie zgadza.

TOmek: ok, dzieki