graniastosłupy aneta: podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9 .Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 60 stopni .Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.

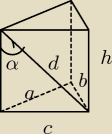
Stachu: Obliczamy długość brakującego boku podstawy graniastosłupa: Trójkąt abc jest prostokątny, a=b=9 więc c²=a²+b² c²=9²+9²=81+81=162 ⇒ c=√162=9√2 Wracamy do graniastosłupa: α=60 stopni Trójkąt jest prostokątny więc c/h=tgα ⇒ 9√2/h=√3 ⇒ h=9√2/√3=9√6/3 P_b=2p*h=(9√2+18)*9√6/3=162√3+162√6/3=54√3=54√6 Teraz obliczamy objętość: V=P_p*h P_p → pole podstawy P_p=1/2*a*H H²=9²−(2√2)²= 81−8=73⇒H=√73 P_p= 1/2*4√2*√73=2√146 V=2√146*9√6/3=12√219 Możliwe są błędy obliczeniowe za co przepraszam ale ogólnie tak trzeba to rozwiązywać Pozdrawiam