prawdopodobieństwo
Ziomal: Proszę o podpowiedz lub pomoc z obliczeniem podpunktu b) P(A∩B') w zadanku poniżej:
zdarzenia A i B zawierają się w przestrzeni zdarzeń Ω a P jest prawdopodobieństwem określonym w
tej przestrzeni. Wiedząc że:
| | 1 | | 1 | | 2 | |
P(A')= |
| ,P(A∩B)= |
| ,P(A∪B)= |
| |
| | 3 | | 4 | | 3 | |
Oblicz:
a)P(B)
| | 1 | | 3 | | 2 | |
tu mi wyszło że P(B)= |
| i P(B')= |
| oraz P(A)= |
| |
| | 4 | | 4 | | 3 | |
b)P(A∩B')
tu nie wiem zbytnio jak się za to zabrać,wie ktoś jak to zrobić ?
13 kwi 22:15
Eta:
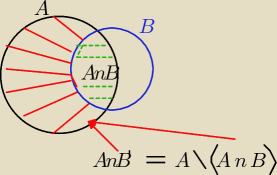
P(A n B
')= P(A)− P(A n B)=........
13 kwi 22:27
Ziomal: Dzięki Eta już kumam..
Ten patent z rysunkami to dobra rzecz.. w końcu te działania na
zbiorach łatwiej ogarnąć z rysunku.
B' to wszystko poza B. wiec cześć wspólna A∩B' to zbiór A − A∩B
13 kwi 22:36
Eta:
13 kwi 22:37
Ziomal: Dodatkowe pytanie jak bym miał policzyć B\A w tym zadanku to może wyjść wynik ujemny? =>
P(B\A)=0 bo prawdopodobieństwo nie może być ujemne? Czy raczej ja coś źle policzyłem i nie
powinno nic takiego wychodzić i jak już to idealnie ma się wyzerować
13 kwi 23:18
Eta:
Nie może
!
13 kwi 23:19
Eta:
Narysuj zbiory
zobaczysz,ze :
B \ A = B \ (A ∩ B)
P(B\A) = ....... =0
13 kwi 23:22
Ziomal: Fakt
Dzięki jeszcze raz.Spadam spać ,jutro rano do szkoły muszę wstać.
dobranoc
13 kwi 23:30
Eta:
Miłych snów
..........nie tylko o zbiorach
13 kwi 23:31