pomoc mycha: Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 4. Dwie ściany boczne tego ostrosłupa są prostopadłe do płaszczyzny podstawy, a trzecia tworzy z płaszczyzną podstawy kąt o mierze 60°. oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

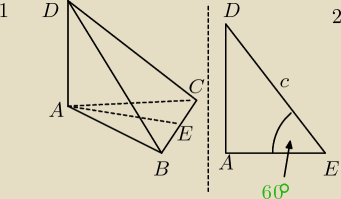
Wojteq66: Wiemy że AE=4 (bok trójkąta) oraz znamy kąt AED Musimy wyliczyć wysokośc trójkąta w podstawie aby skorzystać później ze związku trygonometrycznego.

	a√3
h=		= 2√3
	2

Możemy więc z tg60 obliczyć wysokośc (AD) ostrosłupa.

	AD
tg60=
	AE

	AD
√3=
	4

AD= 6 Bez problemu liczysz objętość

	1		a2√3
V=		*		* AD =4√3*6 24√3 [j3]
	3		4

Do pola powierzchni całkowitej potrzebne Ci są jeszcze krawędź DB oraz DE (wysokośc trójkąta BDC)

	a√3
Pole podstawy wynosi		= 4√3
	4

Natomiast żeby wyliczyć pole bocznej, musisz znać pola trójkątów ABD i ACD (są one takie same) P_ABD=P_ACD= 4*6=24 Oraz pole trójkąta BCD Do tego będzie potrzebna wysokośc trójkąta BCD, lczysz ją z tw. Pitagorasa: 6² +(2√3)² = c² c²= 48 => c= 4√3

	4*4√3
PAED=		= 8√3
	2

Więc Pole boczne to: P_ABD + P_ACD + P_BCD=2*24 + 8√3=48+8√3 P_c= P_p + Pb= 4√3 + 48+8√3 = 48 + 12√3 [j²] Mogłem się gdzieś walnąć

Wojteq66: Tam w obliczeniu objętośc finalnie źle obliczyłem, powinno być V=4√3 [j³]