rozwiąż nierówność Werutka: x² > 3x − jak to rozwiązać ?:(

ICSP: x² − 3x >0 ⇔ x(x−3)> 0 ⇔ x ∊ (−∞;0) unia (3;+∞)

M4ciek : x² > 3x x² − 3x > 0 x(x − 3) > 0 x ∊ (−∞,0) ∪ (3,+∞)

Artur: x² − 3x > 0 x(x−3) >0 x=0 x= 3 x∊ (−∞ 0) u (3.+∞)

ICSP: Hahaha pierwszyD

Werutka: dziękuję

Werutka: mam jeszcze jeden problem, a mianowicie 2x³−x²+18−9=0 − polecenie to rozwiąż równanie

ICSP: 2x³ − x² + 18x − 9 = x²(2x−1) +9(2x−1) = (x²+9)(2x−1)

	1
(x2+9)(2x−1) = 0 ⇔ x2 + 9 = 0 v 2x−1 = 0 ⇔ x =
	2

ICSP: x sam sobie dopisałem.

M4ciek : 2x³ − x² + 18x − 9 = 0 x²(2x − 1)+ 9(2x − 1) = 0 (x² + 9) * (2x − 1) =0

	1
x =
	2

M4ciek : Wrrr ICSP

bart: Wy się ścigacie?

Maciuś: dajcie jakies trudne zadanie niech sie poscigaja

ICSP: na to wygląda

M4ciek : Nie , ale ICSP tam widze zaciesza powyzej

ICSP: nie wystarczy cos takiego: dla M4cka: rozłóż na czynniki: x² + 9 Niech się wykaże

M4ciek : Zajrzyj do mojego i pomoz lepiej

:>: Zakładam, że po 18 jest x. x²(2x−1) + 9(2x−1)=0 (x² + 9)(2x−1) = 0 x²+9=0 − sprzecznosc v 2x−1=0

	1
x=
	2

:>: Zakładam, że po 18 jest x. x²(2x−1) + 9(2x−1)=0 (x² + 9)(2x−1) = 0 x²+9=0 − sprzecznosc v 2x−1=0

	1
x=
	2

M4ciek : ICSP kpisz ze mnie x² + 9 = 0 x² = −9 Kwadrat liczby jest zawsze ≥ 0 Takie chce na maturze

Werutka: 1) 3x² − 8x − 3 ≤ 0 ? 2) (x+1) (x−3) > 0 ? polecenie to rozwiąż równanie

M4ciek : Moze bys sie sama nauczyla wkoncu

Ireneusz:

	1
1) x∊≤−		;3≥
	3

Werutka: przepraszam, nierówność

Ireneusz: x∊(−∞;01)U(3;+∞)

ICSP: rozumiem: (x−√6x + 3)(x+√6x + 3). Wymnóż to i powiedz co wyjdzie

Werutka: skoro z Ciebie taki kozak to wytłumacz jak się to robi bo do tej pory nikt nie jest w stanie tego zrobić

Ireneusz: Takie zadanka się w głowie liczy Fajna rozgrzewka dla mózgu ^^

Ireneusz: Werutka w pierwszym przykładzie liczysz wyróżnik trójmianu a następnie jeśli jest większe od zera to jego pierwiastki. Jeśli już je masz to zaznaczasz je na osi i rysujesz wykres w zależności od znaku przy najwyższej potędze i odczytujesz przedziały...

Ireneusz: @ICPS to jest równe x²+9 ^^

ICSP: przecież wiem

Werutka: też bym tak chciała

Ireneusz: Werutka moja mała rada. Wypożycz sobie jakiś zbiór zadań i rozwiązuj, rozwiązuj rozwiązuj i jeszcze raz rozwiązuj. W pewnym momencie zaczniesz "widzieć" rozwiązania w mniej skomplikowanych przykładach, a i trudniejsze nie będą sprawiać Ci problemów

Werutka: problem jest w tym że ja nie mam zielonego pojęcia jak się za to zabrać, jak widze pierwiastki to pierwsza myśl jaka mnie ogarnia to: nie umiem !, jest ze mnie niezły tuman

Ireneusz: Musisz myśleć pozytywnie... Zacznij od łatwych przykładów i później zwiększaj stopień trudności

Werutka: ja mam bardzo dobrą pamięć, mogę nawet sie pochwalić jakie zrobiłam błędy na poprzednim sprawdzianie. Chodzi mi o to, że nikt mi nie jest wstanie wytłumaczyć pewnego schematu do zadań, bo przecież wszystkie rozwiązania to pewien schemat... Gdyby ktoś mi go pokazał zapamiętałabym go i w ten sposób mogłabym wszystko rozwiązywać

Ireneusz: Werutka ciężko jest to tak wytłumaczyć pisząc, ale głównie polega to na tym, żeby powyłączać coś przed nawias, korzystać ze wzorów skróconego mnożenia, sprowadzać do stopnia drugiego i liczyć deltę, oraz na grupowaniu wyrazów. Jak masz coś po różnych stronach np. równania, to przenosisz wszystko na jedną stronę i segregujesz od największej potęgi do najmniejszej i starasz się wyliczyć tego iksa

Werutka: eh nie łatwo być humanistką i walczyć z matmą no nic, będe walczyć do upadłego dziękuję

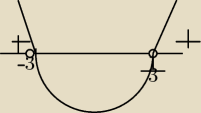
Ireneusz: 3x²−3>−8x −> Przenosisz na lewą stronę −8x i zmieniasz znak 3x²+8x−3>0 −> Liczysz deltę, żeby sprawdzić czy ma pierwiastki to równanie. Jeżeli delta>0 to ma 2 pierwiastki, a jeśli =0 to jeden podwójny. Największa potęga mówi Ci ile równanie ma rozwiązań)

	−b +−√Δ
Δ=82−4*3*(−3)=100 −> √Δ=10, więc x1/2=		i Liczysz je.
	2a

	1
x1=−3 v x2=		. W tym momencie musisz te punkty zaznaczyć na osi, żebyś mogła odczytać z
	3

wykresu przedziały dla których argumentów funkcja przyjmuje wartości dodatnie. Zaznaczyłem ci

	1
je plusami. I teraz odczytujesz przedział x∊(−∞;−3)U(		;+∞) Przedziały otwarte, ponieważ
	3

mają być tylko większe od 0 a nie równe i większe.

ukasz: Werutka, nauczę Cię matmy, a Ty za mnie przeczytaj lektury do prezentacji, jak humanistką jesteś, bo żadnej jeszcze nie ruszyłem

Werutka: jakie masz lektury ?

ukasz: ojj.. Makbeta, Antygone, Dziady III, (Król z żelaza, Prywatne życie Stalina)^{poza kanonem lektur}

ukasz: Wszystko to o Bohaterze despotycznym w literaturze <3 Szkoda, że żadnego malarstwa, albo filmu nie wziąłem

Werutka: hm z dziadków teraz mamy powtórkę, antygony i magbeta nie czytałam, ale wiem o co tam chodzi pod tym kątem funkcje wymierną lubisz ?

ukasz: Funkcja wymierna to moje drugie imie

Werutka: chcesz się trochę pobawić i wytłumaczyć mi rzeczy oczywiste ?

ukasz: A widzisz... pomocy nigdy nie odmówię Mów czego nie wiesz

Werutka: nie mam zielonego pojęcia jak odczytać własności, obliczyć miejsce 0 funkcji która ma postać

	a
f(x)=		−1 wiem jedynie że przy wykonywaniu rysunku −2 zamieniam na +2
	x−2

Werutka: a i wiem że równanie asymptot to y= −1 , x = 2 − tak?

ukasz:

	a
f(x) =		−1.
	x−2

1. Ustalamy dziedzinę funkcji, czyli wszystkie argumenty, które nie należą do tej funkcji. Korzystamy ze znanego przysłowia o nie−dzieleniu przez zero Czyli sprawdzamy jaki nie moze być x, aby nie dzielić przez zero.. x−2 = 0 x = 2 Czyli wszystkie liczby spełniają to równanie, oprócz 2. Co zapisujemy: x∊D=R/{2}. 2. Żeby odczytać własności funkcji i obliczyć miejsce zerowe musimy znać wartośc parametru a Ale trzeba obliczyc f(x) = 0

Werutka: a = −2 ?

ukasz: pod a podstawiasz jakąs liczbę. Możemy rozpatrzeć a=−2

Werutka: hm, a da radę obliczyć to a? np. dodać stronami 1 po czym pomnożyć przez −2 i jest a= −2, dobrze kminie ?

ukasz: Nie rozumiem.. Co chcesz dodać stronami i mnożyc ?

Werutka: chciałam się zapytać czy z podanego wzoru funkcji da radę obliczyć 'a'

ukasz: Da się, ale trzeba mieć dodatkowe dane Daj moze jakies zadanie, to Ci wyjaśnie dokładnie jak je trzeba rozwiązać

Werutka:

	a
do wykresu należy punkt A=(3,1) a f(x)=		− 1
	x−2

ukasz: No własnie tego punktu trzeba mi było! Do wykresu należy ten punkt, czyli: x,y A=(3,1) − podstawiamy za x liczbę 3 i musi nam wyjśc 1 f(3) = 1 f(3) = U{a}{3−2)−1 − tutaj także musimy podstawić 3 za x. f(3)=f(3), bo to to samo, więc mozemy to zapisać tak:

a
	−1 = 1
3−2

a
	−1=1
1

a−1 = 1 a = 2

Werutka: ok czyli mamy wzór, tabelka, rysujemy hiperbole, i jak odczytać współrzędne ?

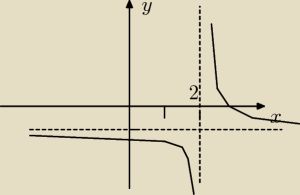
ukasz: Chyba własności

	2
Aby narosywać funkcje f(x) nalezy wykres funkcji		przesunąć o dwie jednoski w prawo i
	x

jedną w dół 1. Dziedzina: x∊D=R / {2}. Widać ładnie na rysunku, że hiperbola nigdy nie przetnie asymptoty pionowej, czyli nigdy nie będzie miała argumentu 2. 2. Zbiór wartości: Zbiorem wartości funkcji jest przedział (−∞;−1) u (−1;+∞). Widać także, że wykres nigdy przyjmie wartości −1. 3. Miejsca zerowe: f(x) = 0 , gdy:

2
	− 1 = 0 |*(x−2) i x≠2
x−2

2 = x−2 x= 4. Miejscem zerowym funkcji jest liczba 4. 4. f(x) > 0 x∊( ) − wszystkie wartości powyżej osi X. To musisz ze swojego wykresu odczytac bo mój to prywizoryczny f(x) = 0 x=4 (to juz obliczylkiśmy) f(x) < 0 ∊∊ ( ) u ( ) 5. Funkcja jest rosnąca w przedziale ∅ Funkcja nie jest stała w żadnym przedziale Funkcja jest malejąca w przedziale (−∞;2) u (2; +∞) − bo 2 wyłaczyliśmy ze zbioru argumentów.

ukasz: 2317990 − jak bedziesz miała jakies zapytania to pisz. Ja juz ide spac, dobrej nocki