:)
M4ciek : Dany jest ciag o wyrazie ogolnym a
n = I n
2 − 90 I − 17
a) Uzasadnij ,ze ciag ten nie jest monotoniczny
b) Znajdz najmniejszy wyraz tego ciagu
a)
a
n + 1 = I(n + 1)
2 − 90I − 17 = In
2 + 2n − 89I − 17
a
n + 1 − a
n = In
2 + 2n − 89I − 17 − ( In
2 − 90I − 17) =
= In
2 + 2n − 89I − 17 − In
2 − 90I + 17 = In
2 + 2n − 89I − In
2 − 90I
I co z tym? Tyle starczy? ,ze roznica a
n + 1 − a
n nie jest rozna od n wiec ciag nie jest
monotoniczny.
b) Nie mam pomyslu
12 kwi 20:55
Aska: jeżeli wynik zależny jest od n czyli nie od stałej wartości to ciąg nie jest monotoniczny
12 kwi 20:58
M4ciek : Dzieki napisalem to 2 linijki wyzej ^^
12 kwi 21:01
ICSP: n
2 − 90 = 0 ⇔ n
2 = 90 ⇔ n = 3
√10(drugie ujemne). Dla takiego argumentu wartosć funkcji
będzie najmniejsza i będzie wynosiła −17
. Jednakże n musi należeć do naturalnych.
√10 ≈ 3,1622776
3
√10 ≈ 9,4868328. Do jakiej liczby naturalnej jest to najbliższe
Oczywiście 10.
Odp. według mnie −7.
12 kwi 21:17
ICSP: Nie umiem przybliżać
Zdarza się
Odp. −8
12 kwi 21:24
M4ciek :
Odp. jest − 8
12 kwi 21:24
ICSP: No co nie umiem przybliżać:( Już się nie śmiać.
12 kwi 21:25
M4ciek :
Czyli :
n
2 − 90 = 0
(n − 3
√10)(n + 3
√10) = 0
n = 3
√10 v n = − 3
√10
Dla n = 3
√10 :
a
n = −17
I tu sie gubie
12 kwi 21:30
M4ciek :
Juz czaje nie pisz
12 kwi 21:32
Eta:
Proponuję skorzystać z wykresu
( jak dla funkcji kwadratowej , tylko dla argumentów naturalnych
Zobaczysz ,że raz ciąg maleje, a następnie rośnie, czyli nie jest monotoniczny
dla n= 9 a
n= |81−90| −17 = 9−17=
−8
dla n=10 a
n= |100−90| −17 = 10−17= −7
itd....
zatem dla n= 9 a
n= −8 −−− to wartość najmniejsza
12 kwi 21:36
M4ciek :
A takie cos :
Dana jest nierownosc :
Ix − 1I + Ix + 2I < m
Wyznacz te wartosci parametru m , dla ktorych ta nierownosc nie ma rozwiazan.
I czy mam to zrobic tak ,ze :
Rysuje wykres y = x −1 oraz y = x + 2.Robie sume wykresow i nierownosc nie bedzie miala
rozwiazan dla m ≤ wykresu
12 kwi 21:51
ICSP: Rozwal na trzy przypadki.
12 kwi 21:51
12 kwi 21:52
M4ciek :
Myslalem ,ze mozna tak , bo ten sposob znam
12 kwi 21:54
M4ciek : Eta jestes jeszcze
12 kwi 22:12
M4ciek : Eta jestes jeszcze
12 kwi 22:13
M4ciek : Podbijam
12 kwi 22:20
M4ciek : Jestes
Eto
12 kwi 22:27
M4ciek : Wrr
Moze jutro Cie zlapie bo mam pytanie.
12 kwi 22:35
Eta:
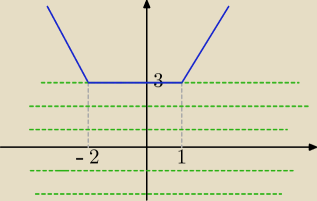
{ −2x −1 dla x < −2
f(x) = { 3 dla −2≤ x <1
{ 2x +1 dla x ≥1
odp:
m < 3
12 kwi 22:48
Eta:
sorry
.......... musiałam coś zjeść,bo przez to forum umrę z głodu
12 kwi 22:51
M4ciek: Hej,Jestes
Eta 
13 kwi 19:17
M4ciek:
Mam 2 pytania :
1.Wracajac do zadania z ciagami , policzylem sobie kolejne liczby naturalne i :
Dla n = 1 , a
n = I1 − 90I − 17 = 72
Dla n = 9 , a
n = I81 − 90I − 17 = −8
Dla n = 11 , a
n = I121 − 90I − 17 = 14
I tyle napisane i zaznaczone kropki na osi wystarczy
2. Zadanie z nierownoscia :
Narysowalas po prostu 3 wykresy w 3 przedzialach i rozumiem ,ze tam jest czesc wspolna wykresow
:
1
o ∩ 2
o ∩ 3
o
I nierownosc bylaby spelniona dla m ≥ 3 i nie spelniona dla m < 3(co nalezalo pokazac)
tak,
13 kwi 19:30
M4ciek: Wpadne pozniej to z pewnoscia odczytam
Pozdrawiam
13 kwi 19:38
M4ciek:
13 kwi 20:04
Eta:
OK
13 kwi 20:07