Okręgi Dawid: Okręgi o równaniach (x−4)²+(y−5)²=25 i (x−7)²+(y−9)²=100 są styczne wewnętrznie. a)oblicz współrzędne punktu styczności tych okręgów. b)Napisz równanie okręgu o możliwie największym promieniu, który jest styczny do jednego z danych okręgów zewnętrznie, a do drugiego wewnętrznie.

Dawid: up

Dawid: up

Bizon: pomogę ...

Dawid: ok czekam

Bizon: do części a) możesz rozwiązać układ równań okręgów

Bizon: a możesz inaczej Napisać równanie prostej przechodzącej przez środki obu okręgów i poszukać puntu wspólnego prostej i obu okręgów

Dawid: co do ukladu rownan nie potrafie wyznaczyc samego x lub samego y.

Dawid: wiec zrobie to ta prosta

Dawid: a co do b jak ?

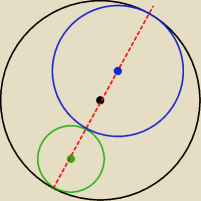
Bizon: to pomoże? ...

Dawid: niebardzo

Bizon: nie żartuj ... promień tego okręgu to ... choć ten rysunek nie w skali

Dawid: ok kumam ten okrag bedzie w srodku i jego promieniem bedzie srednica duzego minuss maleg

Dawid: a jak wyznaczyc srodek ? nie jego promien tylko jego sredniaca

Dawid: a co do liczenia tego punktu prosta to delta mi ujemna wyszla ?

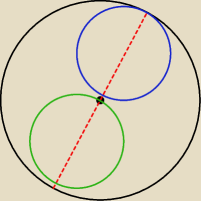
Bizon: dokładnie

Dawid: moge tu dac jeszcze jedno zadanie na temat okregow ?

Bizon: wracając do pierwszego sposobu też da się rozwiązać ... porównasz równania ... po wykonaniu działań x² i y² "poznoszą się" .... z tego co wyjdzie z uproszczeń wyciągniesz np x i wstawisz do któregoś z równań

Dawid: b) zrobilem ale z a) mam problem.

Bizon: coś musiałeś w tych rachunkach "przekręcić" ...

	4		1
Równanie prostej to y=		x−
	3		3

Po wstawieniu do (x−4)²+(y−5)²=25 po przekształceniach otrzymujemy x²−8x+7=0 z tego x₁=1 więc y=1 i szukany punkt np C=(1, 1) z x₂ otrzymamy oczywiście współrzędne środka dużego okręgu