Promień okręgu wpisanego w trójkąt równoboczny jest równy 6. Oblicz tangens kąta Maryś: Promień okręgu wpisanego w trójkąt równoboczny jest równy 6. b) oblicz tangens kąta α=<DAB, gdzie D jest punktem dzielącym bok BC tego trójkąta w stosunku 1:3, licząc od wierzchołka B. z góry dziękuję za pomoc

Eta: Sprawdź, czy napewno dobrze napisana jest treść? bo koszmarne rachunki wychodzą

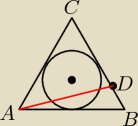
Basia: r = 6

	h
r =
	3

h = 3r h = 18

	a√3
h =
	2

	2h		36		36√3
a =		=		=		= 12√3
	√3		√3		3

	a
DB =		= 3√3
	4

AD² = a² + DB² − 2a*DB*cos60

	1
AD2 = 144*3+9*3 − 2*12√3*3√3*
	2

AD² = 153*3+36*3 = 189*3 = 63*3*3 = 7*9*9 = 7*9² AD = 9√7

sinα		sin60
	=
DB		AD

sinα		√3   2		√3
	=		=
3√3		9√7		18√7

	√3
sinα=		*3√3
	18√7

	9		1
sinα=		=
	18√7		2√7

	1		27		9*3
cos2α= 1 −		=		=
	4*7		4*7		4*7

	3√3
cosα=
	2√7

	1		2√7		1		√3
tgα=		*		=		=
	2√7		3√3		3√3		9

rzeczywiście koszmarne (i licho wie czy się nie pomyliłam)

Basia: oczywiście, że się pomyliłam AD² = 153*3 −36*3 = 117*3 = 39*3*3 = 39*3² AD = 3√39= 3√3√13 i niestety od tego miejsca wszystkie obliczenia trzeba poprawić

sinα		√3
	=
3√3		6√3√13

sinα		1
	=
3√3		6√13

	3√3		√3
sinα =		=
	6√13		2√13

	3		3		49		49
cos2α = 1 −		= 1−		=		=
	4*13		52		52		4*13

	7
cosα=
	2√13

	√3		2√13		√3
tgα =		*		=
	2√13		7		7

teraz chyba jest dobrze może tam miało być r=6√3 rachunki byłyby o wiele prostsze

Maryś: Rany, dziękuję bardzo, męczyło mnie to zadanie okrutnie. Odcinek AD udało mi się wyliczyć, ale w życiu bym nie wpadła na pomysł, żeby twierdzenie sinusów, jedynkę itp. wykorzystywać. Odpowiedź dobrze wyszła, bo taką mam w odpowiedziach Nie wiem jak autor zbioru do tego doszedł, bo punktowane było również wyznaczenie długości odcinków DE, AE i podany jets wynik IDEI=9/2, IAEI=21{3}/2 i za wszelką cenę próbowałam z tym coś wymotać. Dzięki wielkie