Znajdź pierwiastki równania kwadratowego Mateo: przygotowania do matury trwają, 23 dni zostały, a ja jestem w dupie, proszę pomóżcie ... Dla jakich parametrów 'a' równanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki.

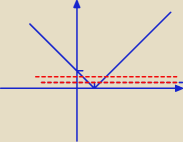
Godzio: 0 < a² − 4a − 1 < 1

Mateo: Godzio, mógłbyś mi to trochę rozjaśnić?

Zongler_Darek: Najpierw założenia: a²−4a−1większe lub równe 0 wychodzi że a należy do <−nieskończoność,2−√5> i <√5+2,nieskończoność> Pierwiastki to 1+a²−4a−1 oraz 1−a²+4a+1 A więc : 1+a²−4a−1>0 wychodzi że a należy do (−nieskończoność,0) i (4, nieskończoność) 1−a²+4a+1>0 wychodzi że a należy do (2−√6,√6+2) A z tego droga już prosta, wyciągamy część wspólną: a należy do przedziału (2−√6,2−√5> i <√5+2,√6+2) Ktoś może sprawdzić

Zongler_Darek: Chciałem dać (2−√6,2−√5) i (√5+2,√6+2) otwarte nawiasy w założeniach też powinny być otwarte.

cvb: zgadzam sie z ostatnim wpisem