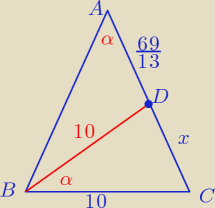
stereometria Patryks: Dany jest trójkąt równoramiennym ABC , w którym |AB | = |AC | i |BC | = 10 . Na boku AC wybrano punkt D w ten sposób, że |∡CBD | = |∡BAC | = α oraz |AD | = 69/13 . Oblicz sin α .

Patryks: może ktoś pomoc ?

kon: mi wyszło √2/2

kon: cofam

Godzio:

	α
|∡BCD | = 90 −
	2

	α		α
|∡CDB | = 180 − α − 90 +		= 90 −		⇒ |∡CDB | = |∡BCD | ⇒ |BC| = |BD|
	2		2

x		10
	=
10		69   + x 13

69
	x + x2 = 100
13

	100
13x2 + 69x − 1300 = 0 ⇒ x =
	13

5² + h² = 13² h² = 144 h = 12

	1		120
P = 60 =		sinα * 132 ⇒ sinα =
	2		169

Eta: OK