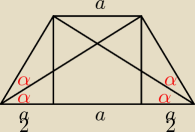
:) M4ciek: W trapezie rownoramiennym jedna z podstaw jest dwa razy dluzsza od drugiej.Przekatna trapezu dzieli kat przy dluzszej podstawie na polowy.Znajdz dlugosci bokow trapezu wiedzac, ze jego pole jest rowne 3√3. P = 3√3

	(a + 2a)*h
P =
	2

	3a*h
3√3 =
	2

6√3 = 3a*h 2√3 = a*h I moje pytanie brzmi z czego tu wyznaczyc drugie rownanie Zeby miec z niego a lub h . Pozdrawiam

M4ciek: Podbijam

JOHNY: BARDZO PROSE "GENIUSZU" NAUCZ SIE LICZYĆ .A NIE !

JOHNY: ℛ

M4ciek: O Co Ci chodzi

JOHNY: hmmmmmmm

M4ciek:

M4ciek: Podbijam

Kejt: może coś z podobieństwa trójkątów..?

M4ciek: Tylko co?

Kejt: a skąd mam wiedzieć? na Mateusza czekam(zadanie z chemii)..nie mam dziś głowy do matmy..

M4ciek: Może ktoś inny coś podpowie ?

Grześ: a to, że kąty między górną podstawą a przekątnymi są takie same. Zaraz to narysuje i pokażę rozwiązanie

kachamacha: kąt między przekątną a krótszą podstawą jest równy α czyli mamy Δ równoramienny tak że ramię jest równe górnej podstawie

kachamacha:

	1
więc h2+(		)2=a2
	2

	√3
h=		a
	2

kachamacha: i już dalej z górki

Grześ: Teraz zależności:

	x
tgα=
	a

	y
tgα=		, czyli:
	a/2

x		y
	=
a		a/2

x=2y Czyli wysokość ma dł. h=3y, tylko teraz zastanawiam się jak się jej pozbyć...

Grześ: aaa.. fakt z Pitagorasa.. ale poszedłem na głeboką wodę

M4ciek: Tylko co mi daje te h = 3y ?

Kejt: Maćku.. patrz komentarz wyżej (kachamacha)

M4ciek:

	1
A skąd się wzięła u kachamachy ta		?
	2

M4ciek: Coś nie łapie

M4ciek: Może ktoś mi coś powiedzieć odnośnie tego Pitagorasa kachamachy?

kachamacha:

	1
miało być		a
	2

M4ciek: A czaję już ehh

Iza: jak przekatna dzieli kat przy dluzszej podstawie na 2 rowne, a jedna podstawa jest 2 razy dluzsza od drugiej, to zawsze ramie wynosi tyle co krotsza podstawa, w tym przypadku 2.

jarolcia: raniona mają długość a ponieważ kąty przy podstawie trójkąta są takie same. i teraz korzystamy 2 razy z twierdzenia pitagorasa.. dla małego trójkąta przy ramieniu i dla trójkąta zawierającego wysokość przekątną i 3/4podstawy