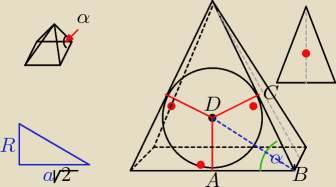
 W ostrosłupie prawidłowym czworokątnym wysokość jest równa H, a krawędź boczna tworzy z
krawędzią podstawy kąt α . Oblicz pole powierzchni kuli wpisanej w ten ostrosłup.α
−−−−−−−−−−−−−−−−−−−−−−−
tylko potrafie zrobic rysunek, choć koło powinno byc bardziej na srodku podstawy, nie wiem co
dalej jakies podobienstwo trójkątow... brak pomyslow
W ostrosłupie prawidłowym czworokątnym wysokość jest równa H, a krawędź boczna tworzy z
krawędzią podstawy kąt α . Oblicz pole powierzchni kuli wpisanej w ten ostrosłup.α
−−−−−−−−−−−−−−−−−−−−−−−
tylko potrafie zrobic rysunek, choć koło powinno byc bardziej na srodku podstawy, nie wiem co
dalej jakies podobienstwo trójkątow... brak pomyslow 






 Bo mi sie wydaje ,ze to wykracza poza matur. roz.
Bo mi sie wydaje ,ze to wykracza poza matur. roz.


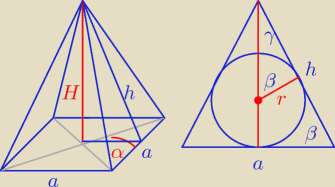
| h | ||||||||
tgα = | ||||||||
|
| 1 | ||
h = | tgα * a | |
| 2 |
| 1 | ||
H2 + ( | a)2 = h2 | |
| 2 |
| 1 | 1 | |||
H2 + | a2 = | a2 * tg2α | ||
| 4 | 4 |
| 1 | 1 | |||
H2 = | a2 * tg2α − | a2 | ||
| 4 | 4 |
| 1 | ||
H2 = | a2(tg2α − 1) | |
| 4 |
| 4H2 | |
= a2 | |
| tg2α − 1 |
| 2H | ||
a = | ||
| √tg2α − 1 |
| Htgα | ||
h = | ||
| √tg2α − 1 |
| aH | ||
PΔ = | ||
| 2 |
| 2P | aH | |||
r = | = | = | ||
| a + b + c | a + 2h |
| ||||||||||||||
= | = | |||||||||||||
|
| 2H2 | H | |||
= | = | |||
| 2H + 2Htgα | 1 + tgα |
| 4πH2 | |
taki mam wynik w odp., podobny, wiec musiałeś cos w obliczeniach sie | |
| (1+tgα)2 |
 teraz trza to przeanalizowac
teraz trza to przeanalizowac 

