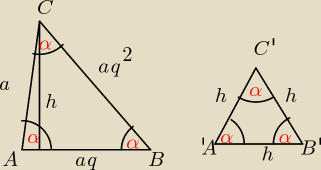
Dan: Długości boków trójkąta ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie q . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta ABC są równe miarom kątów trójkąta ABC . Skoro ten trójkąt ABC ma wysokość równą h, to ten trójkąt A'B'C' jest zbudowany z trzech boków o długości h. A skoro jest to trójkąt równoboczny, to kąty musi mieć rowne 60^o każdy. A skoro z polecenia wynika, że mam udowodnić że te kąty w ABC i A'B'C' są równe to przeprowadzając dowód nie wprost, musimy udowodnić, że trójkąt ABC jest trójkątem równobocznym. A będzie tak tylko wtedy, gdy iloraz q będzie równy 1. Więc a=b=c. Tak wynika z mojego rozumowania. Czyli co mam zrobić? jak to udowodnić ? Dobrze w ogóle myślę ?

Dan: W zasadzie to chyba źle myślę, bo w każdym trójkącie mamy przecież 3 wysokości.

Dan:

Dan:

Dan: odświeżam. Proszę, zerknijcie na to.

Dan:

Dan:

kamis: Oznaczenia: a − a b − aq c − aq²

	a * ha		b * hb		c * hc
Pole trójkąta:		=		=		| * 2
	2		2		2

a * h_a = b * h_b = c * h_c a * h_a = aq * h_b = aq² * h_c |:a h_a = q * h_b = q² * h_c Boki trójkąta A'B'C' w kolejności od najmniejszego: h_c, q * h_c, q² * h_c Stosunek odpowiednich boków ΔABC do ΔA'B'C'

a		a
	=
hc		hc

aq		a
	=
q * hc		hc

aq2		a
	=
q2 * hc		hc

Stosunek tych boków jest taki sam, co oznacza, że ΔABC ~ ΔA'B'C', zatem miary kątów obu trójkątów są takie same.

Dan: czyli jednak zle zrobiłem. racja, są 3 wyskokości. Z sinusów trzeba było to zrobić. Dzięki