Obliczanie pola obszarów mrr: Oblicz pole obszaru ograniczonego krzywymi:

	1
1) y=		, y=x , y=4
	x2

	1
2) y=x2 , y=		x2 , y=3x
	2

Wiem, że z całek. Ale jaką całkę mam ułożyć?

Grześ: narysuj wykresy na jednej osi, potem trzeba znależć punkty w których przecinają się wykresy, chyba będzie ich 4, ale nie jestem pewny. A potem trzeba pole tego obszaru zapisać za pomocą sumy całek. Nie wiem czy jest taki program online, ale te wykresy nie są skomplikowane w rysowaniu. Czyli najpierw je narysuj razem wszystkie i wyznacz wszystkie punkty przecięcia się wykresów. Potem można coś działać

mrr:

	1
1) Przecinają się w (1,1) , (4,4) , (		,4). Zatem jaką całkę ułożyć?
	2

mrrr: ?

mrr: ?

dani: γ=−x²+4x y=x²−4x+10

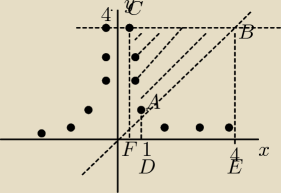
AS: Szukane pole S − pole czworokąta FCBE − pole obszaru FCAD (pod krzywą) − pole trapezu ADBE Współrzędne punktu A znajdujemy z układu równań y = 1/x² i y = x => x = 1/x² => x³ = 1 => x = 1 A(1,1) Współrzędne punktu C z układu równań y = 1/x² , y = 4 =>4 = 1/x² => x = 1/2 , C(1/2,4) Pole czworokąta ECBE = FE*FC = (4 − 1/2)*4 = 14 = S1 Pole trapezu ADEB = (AD + EB)*DE/2 = (1 + 4)*3/2 = 15/2 = S2 Pole pod krzywą FCAD

	x−1		−1
S3 = ∫(1/x2)dx = ∫x−2dx =		=		=
	−1		x

−1		−1
	−		= −1 + 2 = 1
1		1/2

AS: Dok. Szukane pole S = S1 − S2 − S3 = 14 − 15/2 − 1 = 11/2 Całki proszę uzupełnić granicami całkowania od 1/2 do 1