Homy: Dla jakich wartości parametru p równanie |x−15|=p3−4p ma dwa rozwiązania, których iloczyn jest
liczbą dodatnią ?
Proszę o pomoc. Nie rozwiązujcie mi tego zadania. Chciałbym aby mnie ktoś poprowadził jak
go zrobić. Od czego powinienem zacząć ?
9 kwi 20:58
;): Kiedy wartość bezwzględna ma 2 rozwiązania?
9 kwi 21:03
Homy: dla x≥0 i x<0 ? Z definicji
No chyba, że dla (−∞,15) i (15, +∞_
9 kwi 21:14
;): Chyba nie za bardzo |x| > a gdzie a musi być ≥0 żeby mieć co najmniej 1 rozwiązanie więc 2
rozwiązania kiedy będzie miała wartość bezwzględna?
9 kwi 21:20
;): | x | = a
9 kwi 21:21
kamis:
Rozpatrz równanie w dwóch przypadkach, tzn. w których wyrażenie w wartości bezwzględnej
przyjmuje poszczególne wartości i na podstawie wyznaczonych przedziałów rozpatrz prawą stronę
równania.
9 kwi 21:28
Homy: |X| >a ?
9 kwi 21:33
Homy: Nie czaje

Toporny jestem z matmy..

9 kwi 21:36
kamis:
Dla jakich x:
x − 15 < 0
x − 15 ≥ 0
W otrzymanych przedziałach rozpatrz prawą stronę równania.
9 kwi 21:36
kamis:
I oczywiście aby równanie miało sens prawa strona musi przyjmować pewną wartość.
9 kwi 21:38
Homy:

no to tak napisałem przecież na samym początku.

9 kwi 21:41
;): p3 − 4p > 0 wtedy będzie miało 2 rozwiązania
9 kwi 21:43
Homy: no to roziwązanie będzie p∊(−2,0)U(2,+∞) ? I tylko tyle ? I za to 5 punktów ?
9 kwi 21:45
;): Chyba że wolisz rysować wykres funkcji to już jak Ty wolisz
9 kwi 21:46
;): To jest dopiero początek zadania zobacz jaką masz drugą treść zadania
9 kwi 21:47
Homy: a... dobra. Już wiem o co chodzi. Teraz sobie poradzę

nie doczytałem zadania.
Dzięki wszystkim za pomoc

9 kwi 21:49
;): Jeżeli będą jakieś problemy pisz
9 kwi 21:49
Eta:
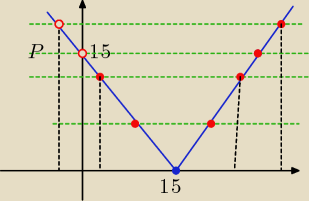
podpowiem tak

1
o p
3−4p >0
2
o y=
m ma z wykresem f(x) = |x−15\
dwa dodatnie rozwiązania <=> gdy m€ (0,15)
czyli wyrazenie po prawej stronie musi być zawarte w tym przedziale
teraz tylko rozwiąż układ:
p
3−4p >0
i
p
3−4p <15
jako odp: podaj część wspólną
otrzymasz odp:
p€ (−2, 0)
powodzenia w rachunkach

9 kwi 22:00
;): p ∊ (−2,0)∪(2,3) taka będzie odpowiedź Eto
9 kwi 22:02
;): x − 15 = p3 − 4p ∨ x − 15 = −p3 + 4p
x = p3 − 4p + 15 ∨ x = −p3 + 4p + 15
z warunku wiemy że liczba p3 − 4p ma być dodatnia więc druga również musi być dodatnia więc
−p3 + 4p + 15 > 0
p3 − 4p − 15 < 0
rozwiązać nierówność i podać cześć wspólna p3 − 4p > 0 ⋀ p3 − 4p − 15 < 0
9 kwi 22:07
Eta:
No tak

niedopisałam tego drugiego przedziału
odp: p€( −2,0) U (2,3)

9 kwi 22:15
;): 
9 kwi 22:17
Eta:
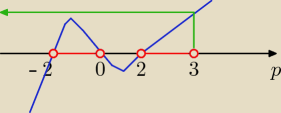

9 kwi 22:25
 Toporny jestem z matmy..
Toporny jestem z matmy.. 
 no to tak napisałem przecież na samym początku.
no to tak napisałem przecież na samym początku. 
 nie doczytałem zadania.
Dzięki wszystkim za pomoc
nie doczytałem zadania.
Dzięki wszystkim za pomoc 
 podpowiem tak
podpowiem tak 1o p3−4p >0
2o y= m ma z wykresem f(x) = |x−15\
dwa dodatnie rozwiązania <=> gdy m€ (0,15)
czyli wyrazenie po prawej stronie musi być zawarte w tym przedziale
teraz tylko rozwiąż układ:
p3−4p >0
i
p3−4p <15
jako odp: podaj część wspólną
otrzymasz odp: p€ (−2, 0)
powodzenia w rachunkach
1o p3−4p >0
2o y= m ma z wykresem f(x) = |x−15\
dwa dodatnie rozwiązania <=> gdy m€ (0,15)
czyli wyrazenie po prawej stronie musi być zawarte w tym przedziale
teraz tylko rozwiąż układ:
p3−4p >0
i
p3−4p <15
jako odp: podaj część wspólną
otrzymasz odp: p€ (−2, 0)
powodzenia w rachunkach

 niedopisałam tego drugiego przedziału
odp: p€( −2,0) U (2,3)
niedopisałam tego drugiego przedziału
odp: p€( −2,0) U (2,3)



