sprawdzic tylko qqqqqqqq: zbiorem rozwiązań nierówności x²≥5 zrobilam tak: x²−5≥0 (x−√5)(x+√5≥0 to jak to wtedy jest x ≥ √5 u x ≤ −√5 czy moze: x ≥ √5 u x ≥ −√5

Rivi: xe(−∞,−√5)u(√5, +∞) jak nie jesteś pewny/pewna to po prostu sprawdź − podstawiasz liczby i jest si. A najlepiej to narysuj "falę"

Rivi: oczywiście przy pierwiastkach ostry nawias <>

qqqqqqqq: ale chodzi o to, ze ja nie rozumiem jak to narysowac kiedy mniejsze a kiedy wiekszebo zapisac bym potrafila x ≥ √5 u x ≤ −√5 to jest dobrze czy moze to x ≥ √5 u x ≥ −√5

qqqqqqqq:

qqqqqqqq: ale z czego to wynika ze x≤−√5 u x≥√5

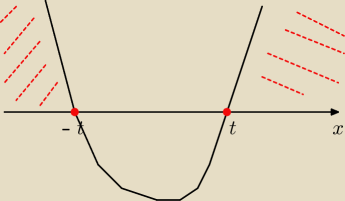
rumpek: x²≥5 x² − 5 ≥ 0 (x − √5)(x + √5) ≥ 0 Rysunek poprawny powyżej Przy x² (tak zwanego a) nie stoi minus więc ramiona w górę (na rysunku moim bo w tym edytorze nie ma pierwiastków to: t = √5 a −t = −√5 Czerwone kreski to to co masz odczytać czyli: x∊(−∞, −√5>U<√5, +∞)

qqqqqqqq: a kiedy sa te "prostokątne" przedziały?

rumpek: Wtedy gdy masz nierówność liniową, np.: 2x + 2 > 0 Jak masz 2x² + 5x − 2 >0 to to co wyżej narysowałem a do wielomianowych to wężyk (z czasem się dowiesz )