trójkąt
rumpek:
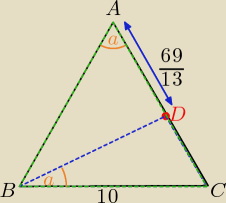
Dany jest trójkąt równoramiennym ABC, w którym |AB| = |AC| i |BC| = 10. Na boku AC
| | 69 | |
wybrano punkt D w ten sposób, że |∡CBD| = |∡BAC| = a oraz |AD| = |
| . Oblicz sinα. |
| | 13 | |
Rysunek dobry zrobiłem?
9 kwi 14:24
rumpek: I kolejne pytanie:
ten odcinek BD u mnie na rysunku jest wysokością trójkąta równoramiennego, tak?
Więc trójkąt DBC jest prostokątny dobrze piszę?
9 kwi 14:42
rumpek: Podpowie ktoś?
9 kwi 15:21
M4ciek:
Wg mnie odcinek BD nie musi byc wysokoscia bo nie wiemy czy jest pod katem prostym?
9 kwi 15:24
rumpek: Jak myślicie można by tu skorzystać z podobieństwa trójkątów

?
9 kwi 16:09
rumpek: Pomocy
9 kwi 16:17
rumpek: Pomoże ktoś?
9 kwi 16:30
rumpek: Podbijamy
9 kwi 16:46
rumpek: Up
9 kwi 17:07
rumpek: Do góry
9 kwi 17:30
rumpek: Pomocy
9 kwi 18:11
TOmek:
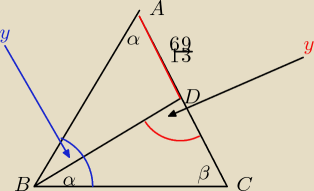
trójkąty BCD i BCA są podobne z cechy k,k,
y=180−(α+β)
9 kwi 18:29
TOmek: no to kombinujemy dalej

9 kwi 18:29
rumpek: Zrobiłeś tylko co ja już mam

9 kwi 18:31
rumpek: Wiesz jak to dokończyć? Czy też nie masz pomysłu

?
9 kwi 18:35
TOmek:
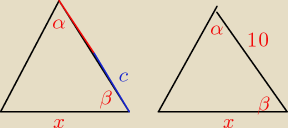
9 kwi 18:37
TOmek: | | α | |
mam pomysl jak to obliczyc dalej, tylko nie wiem czy da sie z sin |
| obliczy sinα xD |
| | 2 | |
9 kwi 18:40
rumpek: Godzio wie na pewno, ale go niestety nie ma

9 kwi 18:41
TOmek: tez czekam na Godzia, bo nie wiem jak jedno zadanko skręcic

9 kwi 18:41
rumpek: A podbije

9 kwi 19:42
rumpek: Eto mogłabyś zerknąć

?
9 kwi 19:51
 Dany jest trójkąt równoramiennym ABC, w którym |AB| = |AC| i |BC| = 10. Na boku AC
Dany jest trójkąt równoramiennym ABC, w którym |AB| = |AC| i |BC| = 10. Na boku AC
 ?
?
 trójkąty BCD i BCA są podobne z cechy k,k,
y=180−(α+β)
trójkąty BCD i BCA są podobne z cechy k,k,
y=180−(α+β)


 ?
?




 ?
?