okreg ast: Napisz równanie okręgu przechodzącego przez punkt P=(1;0) i stycznego do prostych określonych równaniami x+y−2=0 oraz x+y+3−0

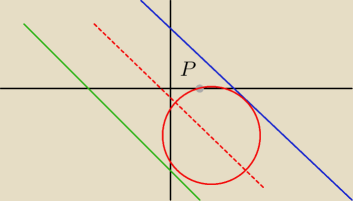
Bizon: Jeśli policzymy odległość między prostymi to poznamy długośc promienia okręgu (połowa

	1
odległości)Środek okręgu będzie leżał na prostej y=−x−		.
	2

Na prostej tej będziemy musieli znaleźć punkt odległy od P o r.... będący środkiem okręgu. Pomagać ...? ... czy sam poradzisz ...

ast: dam radę dzieki wielkie ; )

Magda: Czemu środek okręgu lezy na tej prostej? Prosze o odpowiedz.

Bizon: ... skoro dane proste są równolegle ... to między nie możemy wpisać nieskończenie wiele okręgów stycznych do nich ... środki tych okręgów to zbiór punktów równoodległych od danych prostych (prosta równoległa do danych prostych) Punkt P pozwoli wyznaczyć konkretne okręgi (bo będą dwa)