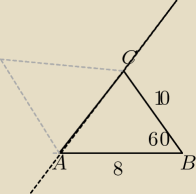
PRoblem TOmek: W trójkącie ABC |AB| = 8, |BC| = 10, zaś |kąt ABC| = 60 stopni. Oblicz objętość i pole powierzchni bryły powstałej z obrotu trójkąta ABC dookoła prostej zawierającej bok AC. −−−−−−−−−− i nie wiem co dalej myślałem coś o polu trójkąta ale nie ma do czego przyrównac...

Godzio : Z tw. cosinusów wylicz 3 bok Ten obrót powoduje powstanie 2 stożków, zaraz zobrazuje

TOmek: ok wiem dzieki za wskazówkę

Godzio :

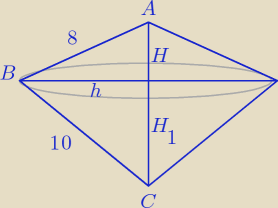
	1
P =		* 8 * 10 * sin60o
	2

|AC|² = 8² + 10² − 2 * 8 * 10 * co60^o ⇒ |AC| = ...

	|AC| * h
P =
	2

1		|AC| * h
	* 8 * 10 * sin60o =		⇒ h = ...
2		2

h² + H₁² = 10² ⇒ H₁ = ... h² + H² = 8² ⇒ H = ... Dalej sobie dasz radę

TOmek: no taki własnie miałem pomysl, dzieki pięknie Godzio

Ann: Proszę o pomoc w obliczeniu powierzchni tej bryły. Liczę i liczę i mi nie wychodzi R=20√7/7 L1=8 L2=10

Ann: muszę to na jutro zrobić a nie wychodzi mi.. Liczę pole "pierwszego" stożka później drugiego i wychodzi mi zły wynik jak dodam.. pomoże ktoś?